| Codeforces Round 914 (Div. 2) |
|---|
| Закончено |
Поскольку Хаяте не получил никаких рождественских подарков от Санты, его вместо этого ожидает решение задачи на запросы на дереве.
У Хаяте есть дерево с $$$n$$$ вершинами.
Теперь Хаяте хочет, чтобы вы ответили на $$$q$$$ запросов. Каждый запрос состоит из вершины $$$x$$$ и $$$k$$$ других дополнительных вершин $$$a_1,a_2,\ldots,a_k$$$. Эти $$$k+1$$$ вершина гарантированно различны.
Для каждого запроса необходимо найти длину самого длинного простого пути, начинающегося в вершине $$$x^\dagger$$$ после удаления вершин $$$a_1,a_2,\ldots,a_k$$$ вместе со всеми ребрами, соединенными хотя бы с одной из вершин $$$a_1,a_2,\ldots,a_k$$$.
$$$^\dagger$$$ Простой путь длины $$$k$$$, начинающийся в вершине $$$x$$$ — это последовательность различных вершин $$$x=u_0,u_1,\ldots,u_k$$$ таких, что существует ребро между вершинами $$$u_{i-1}$$$ и $$$u_i$$$ для всех $$$1 \leq i \leq k$$$.
Первая строка содержит два целых числа $$$n$$$ и $$$q$$$ ($$$1 \le n, q \le 2 \cdot 10^5$$$) — количество вершин дерева и количество запросов.
Следующие $$$n - 1$$$ строк содержат по два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \ne v$$$) — в дереве есть ребро между вершинами $$$u$$$ и $$$v$$$. Гарантируется, что заданные ребра образуют дерево.
Следующие $$$q$$$ строк описывают запросы. Каждая строка содержит целые числа $$$x$$$, $$$k$$$ и $$$a_1,a_2,\ldots,a_k$$$ ($$$1 \leq x \leq n$$$, $$$0 \leq k < n$$$, $$$1 \leq a_i \leq n$$$) — начальная вершина, количество удаленных вершин и удаленные вершины.
Гарантируется, что в запросе все вершины $$$x,a_1,a_2,\ldots,a_k$$$ различны.
Гарантируется, что сумма $$$k$$$ по всем запросам не превосходит $$$2 \cdot 10^5$$$.
Для каждого запроса выведите одно целое число, являющееся ответом на этот запрос.
7 7 1 2 1 3 3 4 2 5 2 6 6 7 2 0 2 1 1 2 2 1 6 3 1 4 3 1 1 5 0 5 2 1 6
3 2 1 4 1 4 1
4 4 1 2 1 3 2 4 2 1 3 3 1 4 2 1 4 2 3 1 3 4
1 2 2 0
В первом примере дерево выглядит следующим образом:
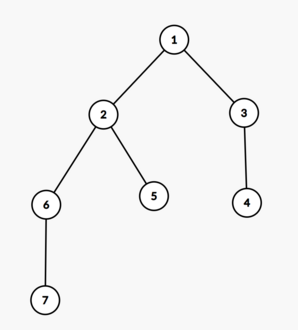
В первом запросе ни одна вершина не пропущена. Самый длинный простой путь, начинающийся в вершине $$$2$$$, это $$$2 \to 1 \to 3 \to 4$$$. Таким образом, ответ — $$$3$$$.
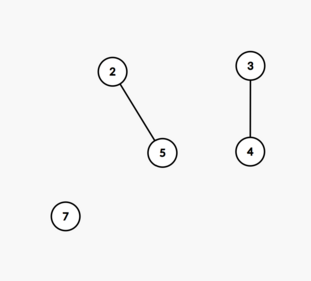
Во третьем запросе отсутствуют вершины $$$1$$$ и $$$6$$$, и дерево показано ниже. Самый длинный простой путь из вершины $$$2$$$ — это $$$2 \to 5$$$. Таким образом, ответ — $$$1$$$.
| Название |
|---|




