| Codeforces Round 121 (Div. 1) |
|---|
| Закончено |
В Берляндии очень беспокоятся о секретности, поэтому почти все планы и схемы всего и вся засекречены. Несмотря на это, шпиону соседнего государства удалось украсть схему метрополитена Берляндска.
В метро Берляндска есть n станций, пронумерованных от 1 до n, и m двусторонних тоннелей, их соединяющие. Все берляндское метро состоит из линий. Если быть более точным, есть два типа линий: кольцевые и радиальные.
Радиальная линия — это последовательность станций v1, ..., vk (k > 1), где станции vi и vi + 1 (i < k) соединены тоннелем, причем никакая станция не входит в состав линии более одного раза (vi ≠ vj при i ≠ j).
Кольцевая линия — это последовательность станций v1, ..., vk (k > 2), где станции vi и vi + 1 соединены тоннелем. Кроме того, станции v1 и vk тоже соединены тоннелем. Никакая станция не входит в кольцевую линию более одного раза.
Заметим, что через одну станцию может проходить любое количество линий.
Согласно берляндским нормативам между двумя станциями не может быть более одного тоннеля и каждый тоннель принадлежит ровно одной линии. Естественно, на каждой линии есть хоть один тоннель. Между любыми двумя станциями есть путь по тоннелям метро. Кроме того, с точки зрения теории графов, метрополитен является вершинным кактусом: если рассмотреть метро как граф, в котором станции являются вершинами, а тоннели — ребрами, то каждая вершина лежит не более чем на одном простом цикле.
К сожалению, на схеме, украденной шпионом, были изображены только станции и тоннели. По ней было невозможно определить, к какой линии относится каждый тоннель. Но для совершения диверсии шпиону необходимо знать, какое минимальное и максимальное количество линий может быть в метро Берляндска.
Помогите ему!
На первой строке записаны два целых числа n и m (1 ≤ n ≤ 105, 0 ≤ m ≤ 3·105) — количество станций и тоннелей, соответственно.
На следующих m строках содержатся по два целых числа — номера станций, которые соединяет соответствующий тоннель. Станции нумеруются целыми числами от 1 до n.
Гарантируется, что в графе, который соответствует метро, нет кратных ребер и петель, что он связен и что он является вершинным кактусом.
Выведите два числа — минимальное и максимальное количество линий, соответственно.
3 3
1 2
2 3
3 1
1 3
8 8
1 2
2 3
3 4
4 5
6 4
4 7
7 2
2 8
2 8
6 6
1 2
2 3
2 5
5 6
3 4
3 5
3 6
Схема метро с минимально возможным количеством линий для второго примера:
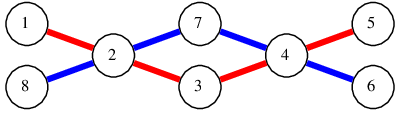
| Название |
|---|




