| Good Bye 2023 |
|---|
| Закончено |
Егор и его друг Арсений в этом году заканчивают учиться в школе и уже скоро поступят университет. И так как они очень ответственные ребята, они начали готовиться к поступлению уже сейчас.
Прежде всего они решили позаботиться о том, где будут жить долгие четыре года обучения, и зайдя на сайт университета, выяснили, что общежитие университета можно представить в виде корневого дерева из $$$n$$$ вершин с корнем в вершине $$$1$$$. В дереве каждая вершина представляет собой рекреацию с некоторым видом активности $$$a_i$$$. Друзьям нужно выбрать $$$2$$$ рекреации (не обязательно различные), в которых они поселятся. Ребята убеждены, что тем будет веселее их жизнь, чем больше значение следующей функции $$$f(u, v) = diff(u, lca(u, v)) \cdot diff(v, lca(u, v))$$$. Помогите Егору и Арсению и найдите максимальное значение $$$f(u, v)$$$ среди всех пар рекреаций!
$$$^{\dagger} diff(u, v)$$$ — количество различных активностей, выписанных на простом пути от вершины $$$u$$$ до вершины $$$v$$$.
$$$^{\dagger} lca(u, v)$$$ — такая вершина $$$p$$$, что она находится на максимальном расстоянии от корня и является предком и вершины $$$u$$$, и вершины $$$v$$$.
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 10^5$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$1 \le n \le 3 \cdot 10^{5}$$$).
Вторая строка каждого набора входных данных содержит $$${n - 1}$$$ целых чисел $$$p_2, p_3, \ldots,p_n$$$ ($$$1 \le p_i \le i - 1$$$), где $$$p_i$$$ — предок вершины $$$i$$$.
Третья строка каждого набора входных данных содержит $$${n}$$$ целых чисел $$$a_1, a_2, \ldots,a_n$$$ ($$$1 \le a_i \le n$$$), где $$$a_i$$$ — номер активности, которая находится в вершине $$$i$$$.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$3 \cdot 10^5$$$.
Для каждого набора входных данных выведите максимальное значение $$$f(u, v)$$$, по всем парам рекреаций $$$(u, v)$$$.
4211 271 1 2 2 3 36 5 2 3 6 5 6131 1 1 2 2 2 3 3 4 5 6 62 2 2 1 4 9 7 2 5 2 1 11 2121 1 1 2 2 3 4 4 7 7 611 2 1 11 12 8 5 8 8 5 11 7
2 9 9 12
Рассмотрим четвертый набор входных данных. Дерево имеет такой вид:
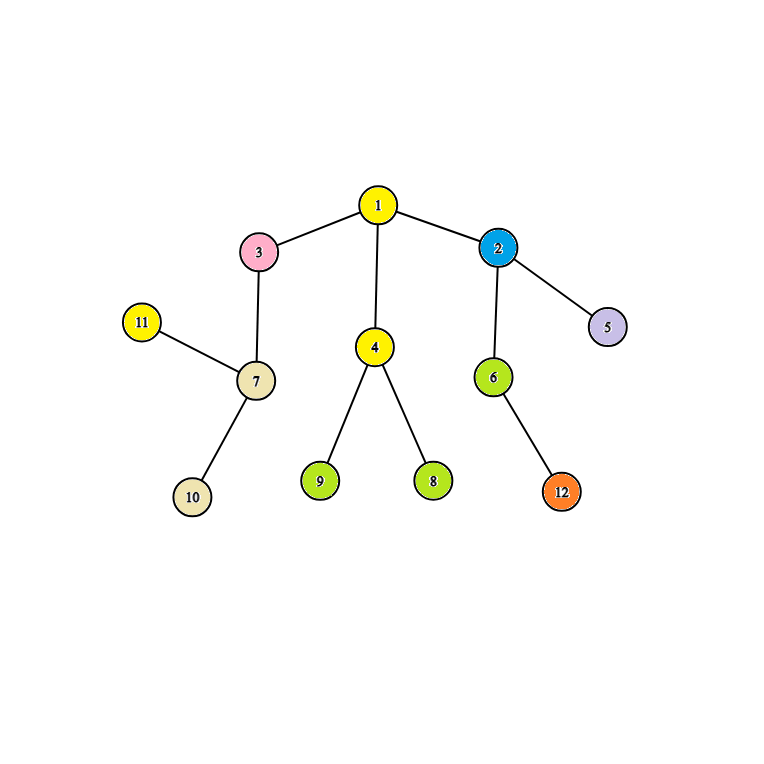
| Название |
|---|




