| Codeforces Round 930 (Div. 2) |
|---|
| Закончено |
Дана таблица размера $$$2 \times n$$$, заполненная нулями и единицами. Пусть число, стоящее на пересечении $$$i$$$-й строки и $$$j$$$-го столбца, равно $$$a_{ij}$$$.
В левой верхней клетке $$$(1, 1)$$$ находится кузнечик, который может прыгать только на одну клетку вправо или вниз. Ему нужно добраться до правой нижней клетки $$$(2, n)$$$. Рассмотрим бинарную строку длины $$$n+1$$$, состоящую из чисел, записанных в клетках пути, без изменения их относительного порядка.
Вам необходимо:
- Найти лексикографически наименьшую$$$^\dagger$$$ строку, которую можно получить, выбрав один из доступных путей;
- Найти количество путей, которые дают эту лексикографически наименьшую строку.
$$$^\dagger$$$ Если строки $$$s$$$ и $$$t$$$ имеют равную длину, то строка $$$s$$$ лексикографически меньше строки $$$t$$$, если и только если в первой позиции, где $$$s$$$ и $$$t$$$ различны, в строке $$$s$$$ элемент меньше, чем соответствующий элемент в $$$t$$$.
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$).
Вторая строка каждого набора входных данных содержит бинарную строку $$$a_{11} a_{12} \ldots a_{1n}$$$ ($$$a_{1i}$$$ равно либо $$$0$$$, либо $$$1$$$).
Третья строка каждого набора входных данных содержит бинарную строку $$$a_{21} a_{22} \ldots a_{2n}$$$ ($$$a_{2i}$$$ равно либо $$$0$$$, либо $$$1$$$).
Гарантируется, что сумма значений $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите:
- Лексикографически наименьшую строку, которую можно получить;
- Число путей, дающих эту строку.
32000041101110080010011111101101
000 2 11000 1 001001101 4
В первом наборе входных данных лексикографически наименьшей строкой является $$$\mathtt{000}$$$. Есть два пути, движение по которым даст эту строку:

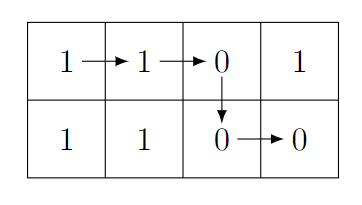
Во втором наборе входных данных лексикографически наименьшей строкой является $$$\mathtt{11000}$$$. Существует всего один путь, дающий такую строку:
| Название |
|---|




