| Codeforces Round 933 (Div. 3) |
|---|
| Закончено |
Рудольф и Бернард решили сыграть с друзьями в игру. В круг встают $$$n$$$ человек и начинают бросать друг другу мяч. Они пронумерованы от $$$1$$$ до $$$n$$$ по часовой стрелке.
Назовём переходом в игре перемещение мяча от некоторого игрока к его соседу. Переход может быть выполнен по часовой стрелке или против часовой стрелки.
Назовём расстоянием по часовой стрелке (против часовой стрелки) от игрока $$$y_1$$$ до игрока $$$y_2$$$ число переходов по часовой стрелке (против часовой стрелки), которые нужно выполнить, чтобы переместить мяч от игрока $$$y_1$$$ к игроку $$$y_2$$$. Например, если $$$n=7$$$, тогда расстояние по часовой стрелке от $$$2$$$ до $$$5$$$ равно $$$3$$$, а расстояние против часовой стрелки от $$$2$$$ до $$$5$$$ равно $$$4$$$.
Изначально мяч находится у игрока номер $$$x$$$ (нумерация игроков осуществляется по часовой стрелке). Во время $$$i$$$-го хода тот, у кого мяч, бросает его на расстояние $$$r_i$$$ ($$$1 \le r_i \le n - 1$$$) по или против часовой стрелки. Например, если играет $$$7$$$ человек, и $$$2$$$-й игрок, получив мяч, бросает его на расстояние $$$5$$$, то мяч получит либо $$$7$$$-й игрок (бросок по часовой стрелке), либо $$$4$$$-й игрок (бросок против часовой стрелки). Иллюстрация этого примера приведена ниже.
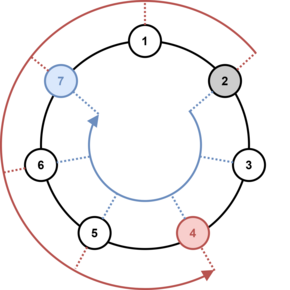
Игра прервалась после $$$m$$$ бросков из-за неожиданного дождя. Когда дождь закончился, ребята вновь собрались, чтобы продолжить. Однако никто не мог вспомнить, у кого остался мяч. Как оказалось, Бернард запомнил расстояния каждого из бросков и направление для некоторых бросков (по часовой стрелке или против часовой стрелки).
Рудольф просит вас помочь ему и на основе информации от Бернарда вычислить номера игроков, у которых мог оказаться мяч после $$$m$$$ бросков.
Первая строка входных данных содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следуют описания наборов.
Первая строка каждого набора содержит три целых числа $$$n, m, x$$$ ($$$2 \le n \le 1000$$$, $$$1 \le m \le 1000$$$, $$$1 \le x \le n$$$) — количество игроков, число совершённых бросков и номер игрока, который бросил мяч первым, соответственно.
Следующие $$$m$$$ строк содержат информацию о каждом броске по порядку. Каждая из них содержит целое число $$$r_i$$$ ($$$1 \le r_i \le n - 1$$$) — расстояние, на которое был совершен $$$i$$$-й бросок, и символ $$$c_i$$$, равный «0», «1» или «?»:
- если $$$c_i$$$='0', то $$$i$$$-й бросок был совершен по часовой стрелке,
- если $$$c_i$$$='1', то $$$i$$$-й бросок был совершен против часовой стрелки,
- если $$$c_i$$$='?', то Бернард не помнит направление, и $$$i$$$-й бросок мог быть совершен как по часовой стрелке так и против часовой стрелки.
Гарантируется, что сумма $$$n \cdot m$$$ ($$$n$$$ умноженное на $$$m$$$) по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите по две строки.
В первой строке выведите количество игроков $$$k$$$ ($$$1 \le k \le n$$$), у которых в конце игры мог оказаться мяч.
В следующей строке выведите $$$k$$$ чисел $$$b_i$$$ ($$$1 \le b_i \le n$$$) — номера игроков в возрастающем порядке. Все номера должны быть различными.
56 3 22 ?2 ?2 ?12 1 23 110 7 42 ?9 14 ?7 02 08 15 ?5 3 14 04 ?1 ?4 1 12 ?
3 2 4 6 1 11 4 3 5 7 9 3 2 3 5 1 3
Ниже приведена иллюстрация трёх бросков для первого набора входных данных примера. Стрелки обозначают возможные направления броска. Серым цветом обозначены игроки, у которых мог оказаться мяч после броска.
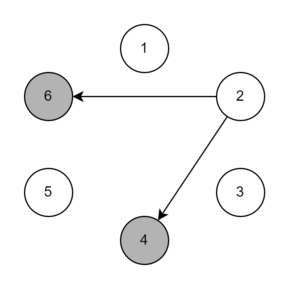
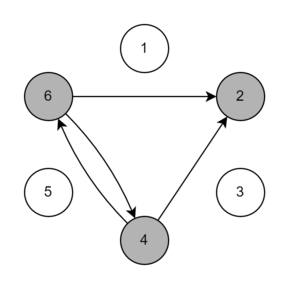
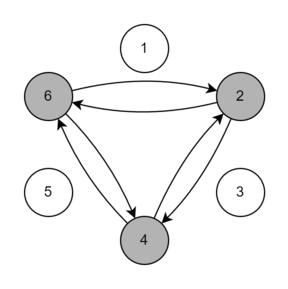
| Название |
|---|




