| Codeforces Round 123 (Div. 2) |
|---|
| Закончено |
Ориентированным взвешенным лесом называется взвешенный ациклический орграф, в котором из каждой вершины выходит не более одного ребра.
Корнем вершины v ориентированного взвешенного леса назовем вершину, из которой не выходит ребра, и до которой можно дойти из вершины v, двигаясь по ребрам ориентированного взвешенного леса. Обозначим корень вершины v как root(v).
Глубиной вершины v назовем сумму весов пути проходящего от вершины v до ее корня. Обозначим глубину вершины v как depth(v).
Рассмотрим процесс построения ориентированного взвешенного леса. Изначально лес не содержит вершин. Вершины последовательно добавляются по одной. Всего выполняется n операций добавления. i-я (i > 0) операция добавления описывается набором чисел (k, v1, x1, v2, x2, ... , vk, xk) и означает, что в граф нужно добавить вершину номер i и k ребер: ребро из вершины root(v1) в вершину i весом depth(v1) + x1, ребро из вершины root(v2) в вершину i весом depth(v2) + x2 и так далее. В случае, если k = 0, в граф добавляется только вершина i и не добавляется никаких ребер.
Ваша задача состоит в том, чтобы по заданным операциям добавления вершин вычислить остаток от деления суммы весов всех ребер леса, получившихся после применения всех заданных операций, на 1000000007 (109 + 7).
В первой строке записано единственное целое число: n (1 ≤ n ≤ 105) — количество операций добавления вершины.
Следующие n строк содержат описание операций, i-я из них содержит описание операции добавления i-ой вершины в следующем формате: первый числом строки является целое k (0 ≤ k ≤ i - 1), далее следует 2k целых чисел, разделенных пробелами: v1, x1, v2, x2, ... , vk, xk (1 ≤ vj ≤ i - 1, |xj| ≤ 109).
Операции заданы в том порядке, в котором их следует применять к графу. Гарантируется, что сумма k по всем операциям не превосходит 105, а также что в результате применения операций добавления вершин не образуется петель и кратных ребер.
Выведите одно целое число — сумму весов всех ребер получившегося графа по модулю 1000000007 (109 + 7).
6
0
0
1 2 1
2 1 5 2 2
1 1 2
1 3 4
30
5
0
1 1 5
0
0
2 3 1 4 3
9
Рассмотрим первый пример:
- Добавляется вершина 1. Так как k = 0, то ребер не добавляется.
- Добавляется вершина 2. Так как k = 0, то ребер не добавляется.
- Добавляется вершина 3. k = 1. v1 = 2, x1 = 1. Добавляется ребро из вершины root(2) = 2 в вершину 3 веса depth(2) + x1 = 0 + 1 = 1.
- Добавляется вершина 4. k = 2. v1 = 1, x1 = 5. Добавляется ребро из вершины root(1) = 1 в вершину 4 веса depth(1) + x1 = 0 + 5 = 5. v2 = 2, x2 = 2. Добавляется ребро из вершины root(2) = 3 в вершину 4 веса depth(2) + x1 = 1 + 2 = 3.
- Добавляется вершина 5. k = 1. v1 = 1, x1 = 2. Добавляется ребро из вершины root(1) = 4 в вершину 5 веса depth(1) + x1 = 5 + 2 = 7.
- Добавляется вершина 6. k = 1. v1 = 3, x1 = 4. Добавляется ребро из вершины root(3) = 5 в вершину 6 веса depth(3) + x1 = 10 + 4 = 14.
Получившийся граф показан на иллюстрации ниже: 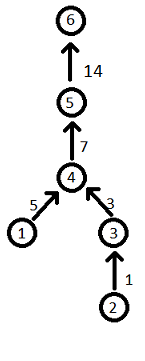
| Название |
|---|




