| Codeforces Round 937 (Div. 4) |
|---|
| Закончено |
Найдите минимальную высоту корневого дерева$$$^{\dagger}$$$ с $$$a+b+c$$$ вершинами, которое удовлетворяет следующим условиям:
- $$$a$$$ вершин имеют ровно $$$2$$$ потомка,
- $$$b$$$ вершин имеют ровно $$$1$$$ потомка, и
- $$$c$$$ вершин имеют ровно $$$0$$$ потомков (не имеют потомков).
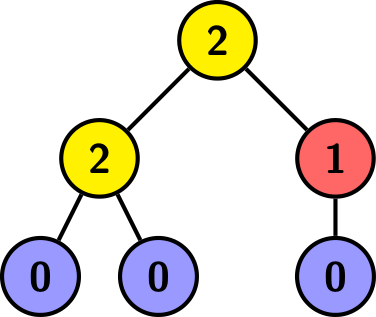
Дерево выше с корнем в верхней вершине, и каждая вершина помечена числом потомков. Здесь $$$a=2$$$, $$$b=1$$$, $$$c=3$$$, и высота равна $$$2$$$.
$$$^{\dagger}$$$ Корневое дерево — это связный граф без циклов, с особой вершиной, называемой корнем. В корневом дереве, среди любых двух вершин, соединенных ребром, одна вершина является родителем (ближе к корню), а другая — потомком.
Расстояние между двумя вершинами в дереве — количество ребер в кратчайшем пути между ними. Высота корневого дерева — это максимальное расстояние от вершины до корня.
Первая строка содержит целое число $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — количество наборов входных данных.
Единственная строка каждого набора входных данных содержит три целых числа $$$a$$$, $$$b$$$, и $$$c$$$ ($$$0 \leq a, b, c \leq 10^5$$$; $$$1 \leq a + b + c$$$).
Сумма $$$a + b + c$$$ по всем наборам входных данных не превышает $$$3 \cdot 10^5$$$.
Для каждого набора входных данных, если такое дерево не существует, выведите $$$-1$$$. В противном случае выведите одно целое число — минимальную высоту дерева, удовлетворяющего описанным условиям.
102 1 30 0 10 1 11 0 21 1 33 1 48 17 924 36 481 0 00 3 1
2 0 1 1 -1 3 6 -1 -1 3
Первый набор входных данных изображен в условии. Можно доказать, что высота не может быть меньше $$$2$$$.
Во втором наборе входных данных, можно сформировать дерево с одной вершиной и без ребер. Оно имеет высоту $$$0$$$, что является оптимальным.
В третьем наборе входных данных, можно сформировать дерево с двумя вершинами, соединенными одним ребром. Оно имеет высоту $$$1$$$, что является оптимальным.
| Название |
|---|




