Изменения рейтингов за последние раунды временно удалены. Скоро они будут возвращены. ×

I. Выращивание деревьев
ограничение по времени на тест
5 секунд
ограничение по памяти на тест
512 мегабайт
ввод
стандартный ввод
вывод
стандартный вывод
wowaka ft. Hatsune Miku - Ura-Omote Lovers
ඞ

Вам дан неориентированный связный простой граф с $$$n$$$ вершинами и $$$m$$$ ребрами, где ребро $$$i$$$ соединяет вершины $$$u_i$$$ и $$$v_i$$$. С каждым ребром связаны два положительных параметра $$$a_i$$$ и $$$b_i$$$. Кроме того, вам дано целое число $$$k$$$.

Неотрицательный массив $$$x$$$ длины $$$m$$$ называется генератором $$$k$$$-остовного-дерева, если он удовлетворяет следующим условиям:

  • Рассмотрим неориентированный мультиграф с $$$n$$$ вершинами, в котором ребро $$$i$$$ клонировано $$$x_i$$$ раз (т.е. существует $$$x_i$$$ ребер, соединяющих $$$u_i$$$ и $$$v_i$$$). Можно разбить ребра этого графа на $$$k$$$ остовных деревьев, где каждое ребро принадлежит ровно одному остовному дереву$$$^\dagger$$$.

Стоимость такого массива $$$x$$$ определяется как $$$\sum_{i = 1}^m a_i x_i^2 + b_i x_i$$$. Найдите минимальную стоимость генератора $$$k$$$-остовного-дерева.

$$$^\dagger$$$ Остовное дерево (мульти)графа — это подмножество ребер графа, которые образуют дерево, соединяющее все вершины графа.

Входные данные

Каждый тест состоит из нескольких наборов входных данных. Первая строка содержит целое число $$$t$$$ ($$$1 \le t \le 500$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.

Первая строка каждого набора входных данных содержит три целых числа $$$n$$$, $$$m$$$ и $$$k$$$ ($$$2 \le n \le 50, n - 1 \le m \le \min(50, \frac{n(n - 1)}{2}), 1 \le k \le 10^7$$$) — количество вершин в графе, количество ребер в графе и параметр для генератора $$$k$$$-остовного-дерева.

Каждая из следующих $$$m$$$ строк каждого набора входных данных содержит четыре целых числа $$$u_i$$$, $$$v_i$$$, $$$a_i$$$ и $$$b_i$$$ ($$$1 \le u_i, v_i \le n, u_i \neq v_i, 1 \le a_i, b_i \le 1000$$$) — конечные точки ребра $$$i$$$ и два его параметра. Гарантируется, что граф прост и связен.

Гарантируется, что сумма $$$n^2$$$ и сумма $$$m^2$$$ по всем наборам входных данных не превосходит $$$2500$$$.

Выходные данные

Для каждого набора входных данных выведите одно целое число: минимальную стоимость генератора $$$k$$$-остовного-дерева.

Пример
Входные данные
4
5 5 1
4 3 5 5
2 1 5 7
2 4 6 2
5 3 3 5
2 5 2 9
5 5 3
4 3 5 5
2 1 5 7
2 4 6 2
5 3 3 5
2 5 2 9
2 1 10000000
1 2 1000 1000
10 15 10
7 1 7 6
5 8 6 6
4 8 2 2
4 3 10 9
10 8 3 4
4 6 6 1
5 4 1 3
9 3 4 3
8 3 9 9
7 5 10 3
2 1 3 4
6 1 6 4
2 5 7 3
10 7 2 1
8 2 6 8
Выходные данные
38
191
100000010000000000
2722
Примечание

В первом наборе входных данных допустимым генератором $$$1$$$-остовного-дерева является $$$x = [1, 1, 1, 1, 0]$$$, как показано на следующем рисунке. Стоимость этого генератора равна $$$(1^2 \cdot 5 + 1 \cdot 5) + (1^2 \cdot 5 + 1 \cdot 7) + (1^2 \cdot 6 + 1 \cdot 2) + (1^2 \cdot 3 + 1 \cdot 5) + (0^2 \cdot 4 + 0 \cdot 9) = 38$$$. Можно доказать, что ни один другой генератор не имеет меньшей стоимости.

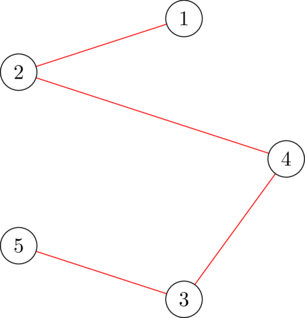Разбиение $$$1$$$-остовного-дерева $$$x = [1, 1, 1, 1, 0]$$$

Во втором наборе входных данных допустимым генератором $$$3$$$-остовного-дерева является $$$x = [2, 3, 2, 2, 3]$$$, как показано на следующем рисунке. Стоимость этого генератора равна $$$(2^2 \cdot 5 + 2 \cdot 5) + (3^2 \cdot 5 + 3 \cdot 7) + (2^2 \cdot 6 + 2 \cdot 2) + (2^2 \cdot 3 + 2 \cdot 5) + (3^2 \cdot 4 + 3 \cdot 9) = 191$$$. Можно доказать, что ни один другой генератор не имеет меньшей стоимости.

Разбиение $$$3$$$-остовного-дерева $$$x = [2, 3, 2, 2, 3]$$$