| Codeforces Round 941 (Div. 1) |
|---|
| Закончено |
На позициях от $$$(1, 1, 1)$$$ до $$$(n, m, 1)$$$ находится $$$n \cdot m$$$ единичных кубиков. Каждый из этих кубиков имеет один из $$$k$$$ цветов. Вы хотите добавить дополнительные кубики в любых целочисленных координатах так, чтобы подмножество кубиков каждого цвета было связано, где два кубика считаются связанными, если они имеют общую грань.
Другими словами, для каждой пары кубиков одного цвета $$$c$$$ должно быть возможно перемещаться от одного к другому, двигаясь только через кубики цвета $$$c$$$, которые имеют общую грань.
Существующие кубики в настоящее время находятся в углу комнаты. Есть бесцветные кубики, полностью заполняющие плоскости $$$x = 0$$$, $$$y = 0$$$ и $$$z = 0$$$, что мешает вам размещать дополнительные кубики там или в отрицательных координатах.
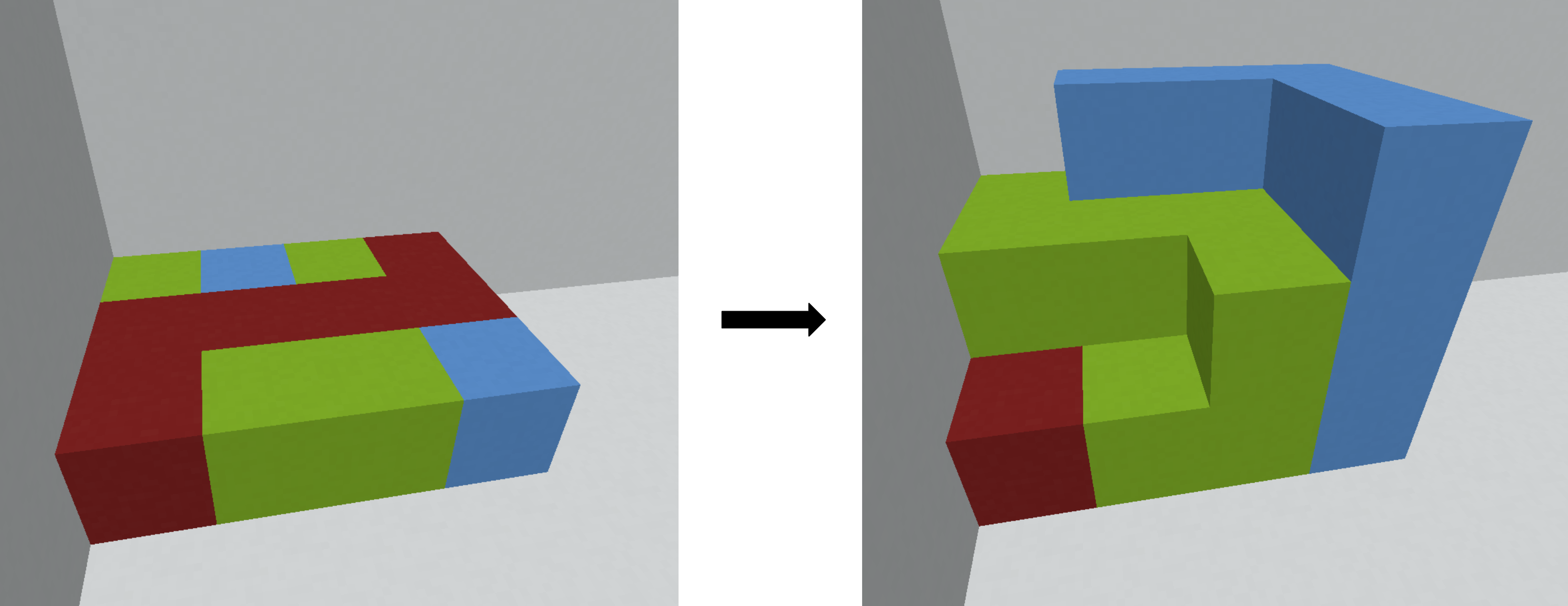
Найдите решение, которое использует не более $$$4 \cdot 10^5$$$ дополнительных кубиков (не включая кубики, которые в настоящее время присутствуют), или определите, что решения нет. Можно показать, что при заданных ограничениях, если есть решение, то оно использует не более $$$4 \cdot 10^5$$$ дополнительных кубиков.
Первая строка ввода содержит три целых числа $$$n$$$, $$$m$$$ и $$$k$$$ ($$$2 \le n, m, k \le 50$$$) — количество строк и столбцов кубиков, и количество цветов, соответственно.
$$$i$$$-я из следующих $$$n$$$ строк содержит $$$m$$$ целых чисел. $$$j$$$-е из них — $$$a_{ij}$$$ ($$$1 \le a_{ij} \le k$$$) — цвет кубика в позиции $$$(i, j, 1)$$$. Для каждого цвета от $$$1$$$ до $$$k$$$ гарантируется, что во входных данных есть как минимум один кубик этого цвета.
Если решения нет, выведите одно целое число $$$-1$$$.
В противном случае, первая строка вывода должна содержать одно целое число $$$p$$$ ($$$0 \le p \le 4 \cdot 10^5$$$) — количество дополнительных кубиков, которые вы добавите.
Следующие $$$p$$$ строк должны содержать четыре целых числа $$$x$$$, $$$y$$$, $$$z$$$ и $$$c$$$ ($$$1 \le x, y, z \le 10^6$$$, $$$1 \le c \le k$$$) — указывая, что вы добавляете кубик цвета $$$c$$$ в позицию $$$(x, y, z)$$$.
Ни у каких двух кубиков в выводе не должны быть одинаковые координаты, и ни один кубик в выводе не должен иметь одинаковые координаты с любым кубиком во входных данных.
Если есть несколько решений, выведите любое.
3 4 33 2 3 11 1 1 11 3 3 2
13 1 1 2 3 1 3 2 3 2 1 2 3 2 2 2 3 2 3 2 3 3 3 2 3 1 2 2 2 1 2 3 2 1 3 3 2 1 4 3 2 2 4 3 2 3 4 3 2 3 4 2 2
2 2 22 11 2
9 1 3 1 1 2 3 1 1 3 1 1 1 3 2 1 1 3 3 1 1 1 1 2 2 1 2 2 2 2 1 2 2 2 2 2 2
Изображение в условии соответствует первому примеру, с $$$\text{красным} = 1$$$, $$$\text{синим} = 2$$$, $$$\text{зеленым} = 3$$$.
| Название |
|---|




