| Codeforces Round 949 (Div. 2) |
|---|
| Закончено |
Обратите внимание на необычное определение $$$\text{MEX}$$$ в этой задаче.
Свинка подарила Черепахе бинарное дерево$$$^{\dagger}$$$ с $$$n$$$ вершинами и последовательностью $$$a_1, a_2, \ldots, a_n$$$ на ее день рождения. Бинарное дерево имеет корень в вершине $$$1$$$.
Если набор путей $$$P = \{(x_i, y_i)\}$$$ в дереве покрывает каждое ребро ровно один раз, то Черепаха считает, что набор путей хороший. Обратите внимание, что хороший набор путей может покрывать вершину дважды или более.
Черепаха определяет значение набора путей как $$$\sum\limits_{(x, y) \in P} f(x, y)$$$, где $$$f(x, y)$$$ обозначает $$$\text{MEX}^{\ddagger}$$$ всех $$$a_u$$$, таких что вершина $$$u$$$ лежит на простом пути от $$$x$$$ до $$$y$$$ в дереве (включая начальную вершину $$$x$$$ и конечную вершину $$$y$$$).
Черепаха задается вопросом о минимальном значении среди всех хороших наборов путей. Пожалуйста, помогите ему вычислить ответ!
$$$^{\dagger}$$$Бинарное дерево — это дерево, в котором у каждой вершины есть не более $$$2$$$ сыновей.
$$$^{\ddagger}\text{MEX}$$$ набора целых чисел $$$c_1, c_2, \ldots, c_k$$$ определяется как наименьшее положительное целое число $$$x$$$, которое не встречается в наборе $$$c$$$. Например, $$$\text{MEX}$$$ для $$$[3, 3, 1, 4]$$$ равно $$$2$$$, $$$\text{MEX}$$$ для $$$[2, 3]$$$ равно $$$1$$$.
Каждый тест содержит несколько тестовых случаев. Первая строка содержит количество тестов $$$t$$$ ($$$1 \le t \le 10^4$$$). Затем следует описание тестов.
Первая строка каждого теста содержит одно целое число $$$n$$$ ($$$2 \le n \le 2.5 \cdot 10^4$$$) — количество вершин в дереве.
Вторая строка каждого теста содержит $$$n$$$ целых чисел $$$a_1, a_2, \ldots, a_n$$$ ($$$1 \le a_i \le 10^9$$$) — элементы последовательности $$$a$$$.
Третья строка каждого теста содержит $$$n - 1$$$ целых чисел $$$p_2, p_3, \ldots, p_n$$$ ($$$1 \le p_i < i$$$) — родитель каждой вершины в дереве.
Дополнительное ограничение на ввод: заданное дерево является бинарным деревом, то есть у каждой вершины не более $$$2$$$ сыновей.
Гарантируется, что сумма $$$n$$$ по всем тестовым случаям не превышает $$$10^5$$$.
Для каждого тестового случая выведите одно целое число — минимальное значение среди всех хороших наборов путей.
553 2 2 1 11 1 2 253 2 1 1 11 1 2 261 2 1 2 1 31 2 3 3 472 1 2 3 1 2 11 1 2 2 3 3101 2 2 1 4 2 3 1 2 11 1 2 2 3 3 4 5 5
4 6 6 6 7
В первом тестовом случае дерево выглядит следующим образом. Число в скобках обозначает вес вершины:
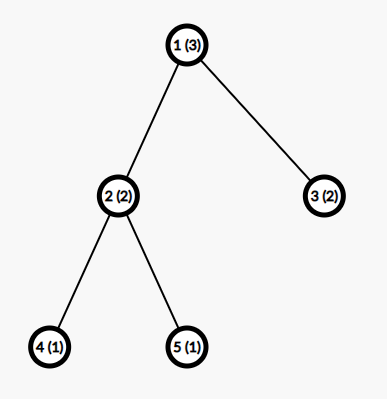
Хороший набор путей с минимальным значением — $$$\{(2, 3), (4, 5)\}$$$.
Обратите внимание, что в этом тестовом случае $$$\{(4, 5)\}$$$ и $$$\{(3, 4), (4, 5)\}$$$ не являются хорошими наборами путей, потому что каждое ребро должно быть покрыто ровно один раз.
Во втором тестовом случае дерево выглядит следующим образом:

Набор хороших путей с минимальным значением — $$$\{(1, 2), (1, 3), (4, 5)\}$$$.
В третьем тестовом случае дерево выглядит следующим образом:

Набор хороших путей с минимальным значением — $$$\{(1, 6), (3, 5)\}$$$.
| Название |
|---|




