| Codeforces Global Round 26 |
|---|
| Закончено |
Две голодные красные панды, Оскар и Лура, получили в подарок дерево $$$T$$$ с $$$n$$$ вершинами. Они хотят выполнить следующую процедуру перемешивания для всего дерева $$$T$$$ ровно один раз. С помощью этой процедуры они создадут новое дерево из вершин старого дерева:
- Выбрать любую вершину $$$V$$$ из исходного дерева $$$T$$$. Создать новое дерево $$$T_2$$$ с $$$V$$$ в качестве корня.
- Удалить $$$V$$$ из $$$T$$$ так, чтобы исходное дерево было разбито на одно или несколько поддеревьев (или ноль поддеревьев, если $$$V$$$ является единственной вершиной в $$$T$$$).
- Перемешать каждое поддерево с помощью той же процедуры (снова выбирая любую вершину в качестве корня), затем соединить корни всех перетасованных поддеревьев с $$$V$$$, чтобы закончить построение $$$T_2$$$.
После этого у Оскара и Луры остается новое дерево $$$T_2$$$. Они могут есть только листья и очень голодны. Поэтому они просят вас помочь им найти максимальное количество листьев среди всех деревьев, которое можно получить за ровно одно перемешивание.
Обратите внимание, что листья — это все вершины со степенью $$$1$$$. Таким образом, корень может считаться листом, если у него есть только один ребенок.
Каждый тест состоит из нескольких наборов входных данных. Первая строка содержит одно целое число $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$2 \leq n \leq 2 \cdot 10^5$$$) — количество вершин в исходном дереве $$$T$$$.
Следующие $$$n - 1$$$ строка содержат по два целых числа $$$u$$$ и $$$v$$$ ($$$1 \leq u, v \leq n$$$), обозначающие ребро в исходном дереве $$$T$$$. Гарантируется, что данные ребра образуют дерево.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$3 \cdot 10^5$$$.
Для каждого набора входных данных выведите одно целое число — максимальное количество листьев, достижимое с помощью одной операции.
451 21 32 42 551 22 33 44 561 21 31 41 51 6109 38 110 68 57 84 61 310 12 7
4 3 5 6
В первом наборе входных данных можно показать, что максимальное количество листьев равно $$$4$$$. Для этого мы можем начать перемешивание с выбора вершины $$$3$$$ в качестве нового корня.
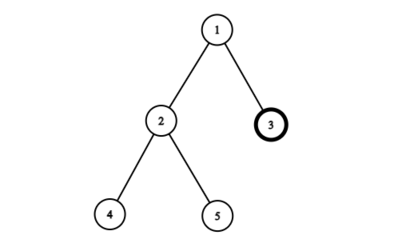
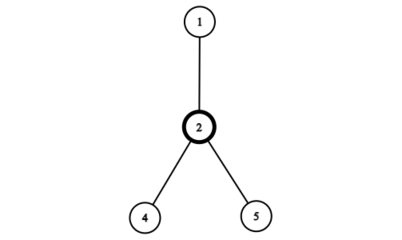
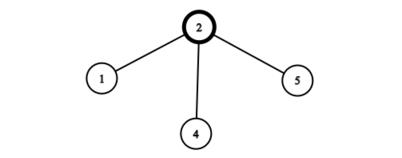
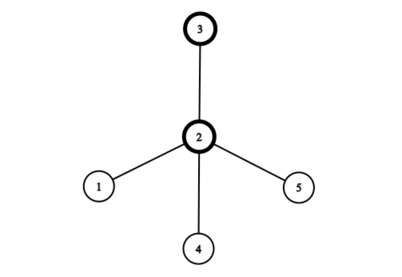
Во втором наборе входных данных у нас есть бамбук из пяти вершин. Можно показать, что максимальное количество листьев после одного перемешивания составляет $$$3$$$. Мы можем начать с вершины $$$2$$$, которая заставит вершину $$$1$$$ стать листом. Затем, если мы выберем вершину $$$4$$$ с правой стороны, вершины $$$3$$$ и $$$5$$$ также окажутся листьями.
Третий набор входных данных представляет собой граф-звезду с шестью вершинами. Количество листьев не может увеличиться, поэтому наш ответ будет равен $$$5$$$ (если мы начнем перемешивание с исходной корневой вершины).
| Название |
|---|




