| Codeforces Round 954 (Div. 3) |
|---|
| Закончено |
Вам дана матрица $$$n \times m$$$, где строки пронумерованы от $$$1$$$ до $$$n$$$ сверху вниз, а столбцы пронумерованы от $$$1$$$ до $$$m$$$ слева направо. Элемент на пересечении $$$i$$$-й строки и $$$j$$$-го столбца обозначим за $$$a_{ij}$$$.
Рассмотрим алгоритм стабилизации матрицы $$$a$$$:
- Найти клетку $$$(i, j)$$$, такую что ее значение строго больше значения всех соседних с ней клеток. Если такой клетки нет, завершить алгоритм. Если таких клеток несколько, то выбирается клетка с наименьшим значением $$$i$$$, а если и таких несколько, то среди них с наименьшим значением $$$j$$$.
- Сделать $$$a_{ij} = a_{ij} - 1$$$.
- Перейти к шагу $$$1$$$.
В этой задаче клетки $$$(a, b)$$$ и $$$(c, d)$$$ являются соседними, если у них есть общая сторона, то есть $$$|a - c| + |b - d| = 1$$$.
Ваша задача вывести матрицу $$$a$$$ после того, как будет запущен алгоритм стабилизации. Можно показать, что данный алгоритм не может выполняться бесконечное количество итераций.
Каждый тест состоит из нескольких наборов входных данных. Первая строка содержит единственное целое число $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — количество наборов входных данных. Далее следует их описание.
Первая строка каждого набора входных данных содержит два целых числа $$$n$$$ и $$$m$$$ ($$$1 \leq n, m \leq 100, n \cdot m > 1$$$) — количество строк и столбцов матрицы $$$a$$$.
Следующие $$$n$$$ строк описывают соответствующие строки матрицы. $$$i$$$-я строка содержит $$$m$$$ целых чисел $$$a_{i1}, a_{i2}, \ldots, a_{im}$$$ ($$$1 \leq a_{ij} \leq 10^9$$$).
Гарантируется, что сумма $$$n \cdot m$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите $$$n$$$ строк по $$$m$$$ чисел в каждой — значения клеток матрицы $$$a$$$ после алгоритма стабилизации.
61 23 12 1112 21 23 42 37 4 51 8 105 492 74 31 7474 92 17 731 17 92 374 7 3 927 31 1 13 31000000000 1 10000000001 1000000000 11000000000 1 1000000000
1 1 1 1 1 2 3 3 4 4 5 1 8 8 74 74 31 31 74 74 17 7 31 17 17 3 31 7 3 3 7 7 1 1 1 1 1 1 1 1 1 1 1
В первом наборе входных данных два раза подряд алгоритм выберет клетку $$$(1, 1)$$$ и завершится.

Во втором наборе входных данных нет клетки, значение которой строго больше значений всех соседних клеток.
В третьем наборе входных данных алгоритм выберет клетку $$$(2, 2)$$$ и завершится.

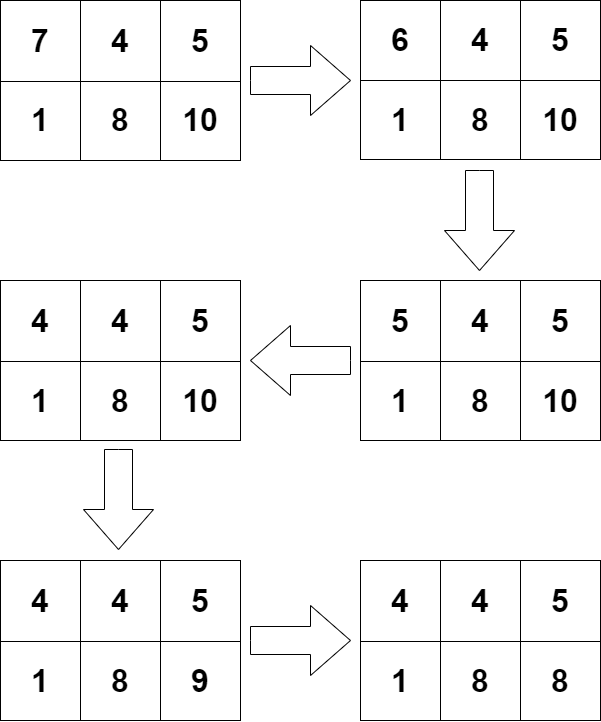
В четвертом наборе входных данных алгоритм три раза выберет клетку $$$(1, 1)$$$ и затем два раза клетку $$$(2, 3)$$$.
| Название |
|---|




