| Codeforces Round 954 (Div. 3) |
|---|
| Закончено |
Вам дан связный неориентированный граф, вершины которого пронумерованы целыми числами от $$$1$$$ до $$$n$$$. Ваша задача минимизировать количество пар вершин $$$1 \leq u < v \leq n$$$, между которыми существует путь в этом графе. Для этого вы можете удалить ровно одно любое ребро из графа.
Найдите это наименьшее количество пар вершин!
Каждый тест состоит из нескольких наборов входных данных. Первая строка содержит единственное целое число $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — количество наборов входных данных. Далее следует их описание.
Первая строка каждого набора входных данных содержит два целых числа $$$n$$$ и $$$m$$$ ($$$2 \leq n \leq 10^5$$$, $$$n - 1 \leq m \leq \min(10^5, \frac{n \cdot (n - 1)}{2})$$$) — количество вершин в графе и количество ребер.
Каждая из следующих $$$m$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \leq u, v \leq n, u \neq v$$$), означающих, что в графе есть неориентированное ребро между вершинами $$$u$$$ и $$$v$$$.
Гарантируется, что данный граф связный и без кратных ребер.
Гарантируется, что сумма $$$n$$$ и сумма $$$m$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите наименьшее количество пар достижимых друг из друга вершин, если можно удалить ровно одно ребро.
62 11 23 31 22 31 35 51 21 33 44 55 36 71 21 32 33 44 54 65 65 51 21 32 32 43 510 121 21 32 32 44 55 66 77 43 88 99 1010 8
0 3 4 6 6 21
В первом наборе входных данных мы удалим единственное ребро $$$(1, 2)$$$ и единственная пара вершин $$$(1, 2)$$$ станет не достижима друг из друга.
Во втором наборе входных данных какое бы ребро мы не удалили, все вершины будут достижимы друг из друга.
В четвертом наборе входных данных так выглядит граф изначально.
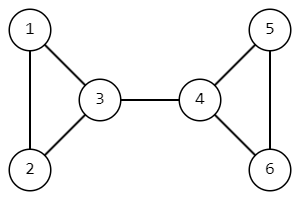
Мы удалим ребро $$$(3, 4)$$$ и тогда достижимы друг из друга будут только пары вершин $$$(1, 2)$$$, $$$(1, 3)$$$, $$$(2, 3)$$$, $$$(4, 5)$$$, $$$(4, 6)$$$, $$$(5, 6)$$$.
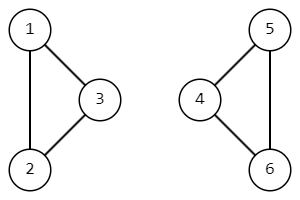
В шестом наборе входных данных так выглядит граф изначально.
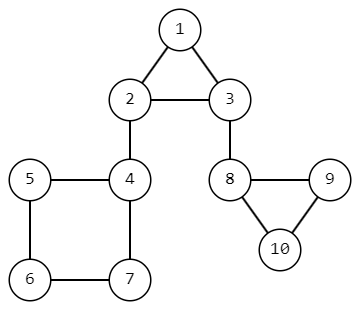
После удаления ребра $$$(2, 4)$$$ граф будет выглядеть следующим образом. Таким образом, будет $$$21$$$ пара достижимых друг из друга вершин.
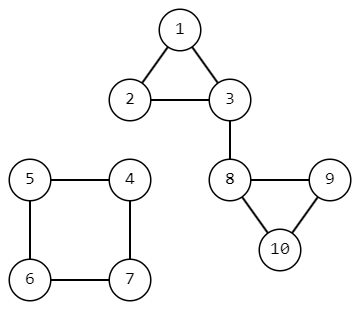
| Название |
|---|




