Дано дерево с $$$n$$$ вершинами с корнем в вершине $$$1$$$, в $$$i$$$-й вершине записано целое число $$$a_i$$$.
Пусть $$$L$$$ — это множество всех прямых сыновей$$$^{\text{∗}}$$$ вершины $$$v$$$. Назовём дерево прекрасным, если для всех вершин $$$v$$$ с непустым $$$L$$$ верно $$$$$$a_v \le \sum_{u \in L}{a_u}.$$$$$$
За одну операцию вы можете выбрать любую вершину $$$v$$$ и увеличить значение $$$a_v$$$ на $$$1$$$.
Найдите минимальное количество операций, необходимых для того, чтобы сделать данное дерево прекрасным!
$$$^{\text{∗}}$$$ Вершина $$$u$$$ называется прямым сыном $$$v$$$, если:
- $$$u$$$ и $$$v$$$ соединены ребром, и
- $$$v$$$ лежит на (единственном) пути от $$$u$$$ до корня дерева.
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 1000$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$2 \le n \le 5000$$$) — количество вершин в дереве.
Вторая строка каждого набора входных данных содержит $$$n$$$ целых чисел $$$a_1, a_2, \ldots, a_n$$$ ($$$0 \le a_i \le 10^9$$$) — значения, написанные на вершинах дерева.
Третья строка каждого набора входных данных содержит $$$n - 1$$$ целых чисел $$$p_2, p_3 , \ldots, p_n$$$ ($$$1 \le p_i < i$$$), каждое из которых означает, что в графе есть ребро между вершинами $$$i$$$ и $$$p_i$$$. Гарантируется, что данные ребра образуют дерево.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$5000$$$.
Для каждого набора входных данных выведите одно целое число — минимальное количество операций, необходимых для того, чтобы сделать данное дерево прекрасным!
459 3 4 1 21 1 3 325 31236 54130 0 01 2
3 2 0 0
Дерево в первом наборе входных данных:
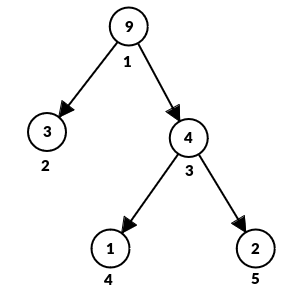
Во втором наборе входных данных вы можете два раза применить операцию к вершине $$$2$$$, чтобы получить прекрасное дерево.
В третьих и четвёртых наборах входных данных дерево уже прекрасно, поэтому применять операций не надо.
| Название |
|---|




