Усадьба плотника Васи отгорожена от леса забором, который состоит из n выстроенных в ряд досок. Забор не замкнут. Доски пронумерованы слева направо от 1 до n, i-ая доска имеет высоту ai. Все доски имеют одинаковую ширину, нижний край каждой доски расположен на уровне земли.
Недавно в местной газете «Малевич и жизнь» написали, что самый модный способ украсить свой забор летом — это нарисовать на нем прямоугольник цвета фуксия, нижняя сторона которого расположена на нижней границе забора.
Вася в восторге от этой идеи! Он немедленно купил краску цвета фуксия и принялся решать, какой именно прямоугольник ему закрасить. Вася точно решил, что закрашенный прямоугольник должен охватывать k последовательных досок. Другими словами, будут окрашены доски с номерами x, x + 1, ..., x + k - 1 для некоторого x (1 ≤ x ≤ n - k + 1). Он хочет закрасить прямоугольник максимальной площади, поэтому высота прямоугольника будет равна min ai для x ≤ i ≤ x + k - 1, x — номер первой окрашенной доски.
Вася уже определился, что ширина прямоугольника может быть равна одному из чисел последовательности k1, k2, ..., km. Для каждого ki он хочет знать математическое ожидание высоты закрашенного прямоугольника, если x для такого забора он выбирает «методом ненаучного тыка» — равновероятно случайно среди всех n - ki + 1 возможных его значений. Помогите ему найти искомые ожидаемые высоты.
В первой строке записано единственное целое число n (1 ≤ n ≤ 106) — количество досок в заборе. Вторая строка содержит последовательность целых чисел a1, a2, ..., an (1 ≤ ai ≤ 109), ai — высота i-й доски забора.
В третьей строке записано целое число m (1 ≤ m ≤ 106), а в следующей строке через пробел записаны m целых чисел k1, k2, ..., km (1 ≤ ki ≤ n), ki — ширина желаемого прямоугольника цвета фуксия в досках.
Выведите m вещественных чисел, разделенные пробельными символами, i-е число равно математическому ожиданию высоты прямоугольника, если его ширина в досках равна ki. Значение будет считаться правильным, если его абсолютная или относительная погрешность не превосходит 10 - 9.
3
3 2 1
3
1 2 3
2.000000000000000
1.500000000000000
1.000000000000000
2
1 1
3
1 2 1
1.000000000000000
1.000000000000000
1.000000000000000
Рассмотрим первый тестовый пример.
- k1 = 1. Всего есть три возможных положения забора. Для первого (x = 1) высота забора равна 3, для второго (x = 2) — 2, для третьего (x = 3) — 1. Так как положение забора выбирается равновероятно случайно, ожидаемая высота забора равна
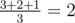 ;
; - k2 = 2. Всего есть два возможных положения забора. Для первого (x = 1) высота забора равна 2, для второго (x = 2) — 1. Ожидаемая высота забора равна
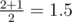 ;
; - k3 = 3. Есть всего одно возможное положение забора. Ожидаемая высота забора равна 1.
| Название |
|---|




