| Codeforces Round 138 (Div. 1) |
|---|
| Закончено |
На плоскости задан не обязательно выпуклый многоугольник без самопересечений, состоящий из n вершин, пронумерованных от 1 до n. На границе многоугольника сидит паук, который может совершать следующие перемещения:
- Переход. Паук из точки p1 с координатами (x1, y1), лежащей на границе многоугольника, перемещается в точку p2 с координатами (x2, y2), также лежащую на границе. При этом он не может покидать границу многоугольника, то есть путь паука от точки p1 к точке p2 проходит вдоль границы многоугольника. Направление обхода границы многоугольника при перемещении (по часовой стрелке или против) паук выбирает сам.
- Спуск. Паук из точки p1 с координатами (x1, y1) перемещается в точку p2 с координатами (x2, y2), при этом точки p1 и p2 должны лежать на одной вертикальной прямой (x1 = x2), точка p1 должна быть не ниже точки p2 (y1 ≥ y2) и отрезок p1p2 не должен иметь точек, находящихся строго вне многоугольника (в частности, отрезок может иметь общие точки с границей).
Изначально паук находится в вершине многоугольника с номером s. Найдите длину кратчайшего пути до вершины с номером t, состоящего из переходов и спусков. Расстояние определяется обычной Евклидовой метрикой 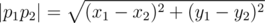 .
.
В первой строке записано целое число n (3 ≤ n ≤ 105) — количество вершин заданного многоугольника. В следующих n строках через пробел записаны по два целых числа — координаты вершин многоугольника. Вершины перечислены в порядке обхода против часовой стрелки. Координаты вершин многоугольника по абсолютной величине не превосходят 104.
В последней строке записаны два целых числа через пробел s и t (1 ≤ s, t ≤ n) — стартовая и конечная вершина искомого кратчайшего пути.
Считайте, что вершины многоугольника пронумерованы в том же порядке, в котором они заданы во входных данных, то есть координаты первой вершины находятся во второй строке входных данных, а n-ой — в (n + 1)-ой строке. Гарантируется, что заданный многоугольник простой, то есть не имеет самопересечений и самокасаний.
В выходной файл выведите единственное вещественное число — длину кратчайшего пути из вершины s в вершину t. Ответ считается правильным, если его абсолютная или относительная погрешность не превосходит 10 - 6.
4
0 0
1 0
1 1
0 1
1 4
1.000000000000000000e+000
4
0 0
1 1
0 2
-1 1
3 3
0.000000000000000000e+000
5
0 0
5 0
1 4
0 2
2 1
3 1
5.650281539872884700e+000
В первом примере паук делает переход по стороне, соединяющей вершины с номерами 1 и 4.
Во втором примере пауку никуда не нужно идти, поэтому расстояние равно нулю.
В третьем примере пауку выгоднее всего перейти из вершины 3 в точку (2,3), совершить спуск в точку (2,1), а затем сделать переход в вершину 1.
| Название |
|---|




