| Codeforces Round 142 (Div. 1) |
|---|
| Закончено |
Алиса и Боб больше не играют ни в какие игры; теперь они дружно изучают свойства различных графов. Алиса придумала следующее занятие: из полного неориентированного графа с n вершинами она выбирает какие-то m ребер и оставляет их себе. Оставшиеся же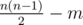 
ребер достаются Бобу.
Алисе и Бобу очень нравятся «треугольники» в графах, то есть циклы длины 3. Поэтому они хотят узнать ответ на такой вопрос: какое суммарное количество треугольников находится в двух графах, образованных ребрами Алисы и ребрами Боба, соответственно?
Первая строка содержит два целых числа n и m (1 ≤ n ≤ 106, 0 ≤ m ≤ 106), разделенные пробелом — количество вершин в изначальном полном графе, а также количество ребер в графе Алисы, соответственно. Далее следуют m строк: i-тая строка содержит два целых числа ai, bi (1 ≤ ai, bi ≤ n, ai ≠ bi), разделенные пробелом — номера двух вершин, соединенных i-тым ребром графа Алисы. Гарантируется, что граф Алисы не содержит кратных ребер и петель. Изначальный полный граф также не содержит кратных ребер и петель.
Считайте, что вершины графа пронумерованы некоторым образом от 1 до n.
Выведите единственное число — суммарное количество циклов длины 3 в графах Алисы и Боба.
Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-битных чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d.
5 5
1 2
1 3
2 3
2 4
3 4
3
5 3
1 2
2 3
1 3
4
В первом примере в графе Алисы есть 2 треугольника: (1, 2, 3) и (2, 3, 4). В графе Боба всего 1 треугольник: (1, 4, 5). Поэтому в двух графах всего 3 треугольника.
Во втором примере в графе Алисы всего 1 треугольник: (1, 2, 3). В графе Боба находится 3 треугольника: (1, 4, 5), (2, 4, 5) и (3, 4, 5). В данном случае ответ на задачу — 4.
