| Codeforces Round 160 (Div. 1) |
|---|
| Закончено |
Максим любит последовательности, особенно те, которые строго возрастают. Сейчас его интересует задача: какова длина самой длинной возрастающей подпоследовательности заданной последовательности a?
Последовательность a задается следующим образом:
- длина последовательности равна n × t;
-
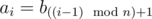(1 ≤ i ≤ n × t), где операция 
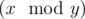обозначает взятие остатка от деления числа x на число y.
Последовательность s1, s2, ..., sr длины r называется подпоследовательностью последовательности a1, a2, ..., an, если найдется такая возрастающая последовательность индексов i1, i2, ..., ir (1 ≤ i1 < i2 < ... < ir ≤ n), что aij = sj. Иными словами, подпоследовательность может быть получена из последовательности путем вычеркивания некоторых элементов.
Последовательность s1, s2, ..., sr называется возрастающей, если выполняется неравенство: s1 < s2 < ... < sr.
У Максима есть k вариантов последовательности a. Помогите Максиму, для каждой последовательности найдите длину наибольшей возрастающей подпоследовательности.
В первой строке заданы четыре целых числа k, n, maxb и t (1 ≤ k ≤ 10; 1 ≤ n, maxb ≤ 105; 1 ≤ t ≤ 109; n × maxb ≤ 2·107). Далее идет k строк, каждая из которых содержит n целых чисел b1, b2, ..., bn (1 ≤ bi ≤ maxb).
Обратите внимание, для всех вариантов последовательности a значения n, maxb и t совпадают, различаются лишь массивы b.
Числа в строках разделяются одиночными пробелами.
Выведите k целых чисел, разделенных пробельными символами — ответы для входных данных. Ответы для каждого варианта последовательности a выводите в порядке следования этих последовательностей во входных данных.
3 3 5 2
3 2 1
1 2 3
2 3 1
2
3
3
