| Codeforces Round 176 (Div. 1) |
|---|
| Закончено |
Джон Доу нашел формулу красивой перестановки.
Рассмотрим перестановку p = p1, p2, ..., pn. Определим преобразование f этой перестановки:
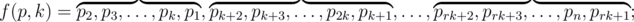
где k (k > 1) — это целое число, параметр преобразования, r — это такое максимальное целое число, что rk ≤ n. Если rk = n, то элементы prk + 1, prk + 2 и далее опускаются. Другими словами, описанное преобразование перестановки p делает циклический сдвиг влево каждого из последовательных блоков длины k, а также последнего блока, длина которого равна остатку от деления n на k.
Джон Доу считает, что перестановка f(f( ... f(p = [1, 2, ..., n], 2) ... , n - 1), n) является красивой. К сожалению, он не может быстро найти интересующую его красивую перестановку. Поэтому он обратился за помощью к Вам.
Вам требуется найти красивую перестановку для заданного n. Для лучшего понимания условия обратите внимание на разбор третьего тестового примера.
В единственной строке записано целое число n (2 ≤ n ≤ 106).
Выведите через пробел n различных целых чисел от 1 до n — красивую перестановку, размера n.
2
2 1
3
1 3 2
4
4 2 3 1
Разберем третий тестовый пример:
- f([1, 2, 3, 4], 2) = [2, 1, 4, 3]
- f([2, 1, 4, 3], 3) = [1, 4, 2, 3]
- f([1, 4, 2, 3], 4) = [4, 2, 3, 1]
| Название |
|---|




