| Codeforces Round 176 (Div. 1) |
|---|
| Закончено |
Как вы знаете, недавно Вова стал новым шаманом города Крайняя Туле. И теперь знание о правильных скобочных последовательностях перешло к нему. Шаманы города Крайняя Туле издавна используют много разных типов скобок. Тип скобки — это целое положительное число. Шаманы определяют правильную скобочную последовательность следующим образом:
- Пустая последовательность является правильной скобочной последовательностью.
- Если {a1, a2, ..., al} и {b1, b2, ..., bk} — правильные скобочные последовательности, то последовательность {a1, a2, ..., al, b1, b2, ..., bk} (их конкатенация) тоже является правильной скобочной последовательностью.
- Если {a1, a2, ..., al} — правильная скобочная последовательность, то последовательность
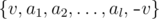 тоже является правильной скобочной последовательностью, где v (v > 0) — целое число.
тоже является правильной скобочной последовательностью, где v (v > 0) — целое число.
Например, последовательности {1, 1, - 1, 2, - 2, - 1} и {3, - 3} являются правильными скобочными последовательностями, а {2, - 3} — нет.
Более того, став шаманом, Вова узнает самую главную правильную скобочную последовательность {x1, x2, ..., xn}, состоящую из n целых чисел. Так как последовательность x — самая главная, Вова решил на всякий случай ее зашифровать.
Шифровка состоит из двух последовательностей. В первой последовательности {p1, p2, ..., pn} записаны типы скобок, то есть pi = |xi| (1 ≤ i ≤ n). Во второй последовательности {q1, q2, ..., qt} записаны t целых чисел — некоторые позиции (возможно не все), на которых в последовательности {x1, x2, ..., xn} стояли отрицательные числа.
К несчастью, Вова забыл самую главную последовательность, но у него сохранилась шифровка: последовательности {p1, p2, ..., pn} и {q1, q2, ..., qt}. Помогите Вове восстановить последовательность x по шифровке. Если существует несколько последовательностей, соответствующих шифровке, нужно восстановить любую, если не существует ни одной требуемой последовательности, нужно об этом сообщить.
В первой строке входных данных записано целое число n (1 ≤ n ≤ 106). Во второй строке записаны n целых чисел: p1, p2, ..., pn (1 ≤ pi ≤ 109).
В третьей строке записано целое число t (0 ≤ t ≤ n) и после него t различных целых чисел q1, q2, ..., qt (1 ≤ qi ≤ n).
Числа в каждой строке отделены друг от друга пробелами.
Выведите единственную строку «NO» (без кавычек), если Вова ошибся, и подходящей последовательности {x1, x2, ..., xn} не существует.
Иначе выведите в первую строку «YES» (без кавычек), а во вторую — n целых чисел x1, x2, ..., xn (|xi| = pi; xqj < 0). Если существует несколько последовательностей, соответствующих шифровке, разрешается вывести любую.
2
1 1
0
YES
1 -1
4
1 1 1 1
1 3
YES
1 1 -1 -1
3
1 1 1
0
NO
4
1 2 2 1
2 3 4
YES
1 2 -2 -1
| Название |
|---|




