| Чемпионат КРОК 2013 - Раунд 1 |
|---|
| Закончено |
В задаче используется упрощенная модель топологий сетей, внимательно прочтите условие задачи и используйте его как формальный документ при разработке решения.
Поликарп продолжает работать системным администратором в некоторой большой корпорации. Компьютерная сеть этой корпорации состоит из n компьютеров, некоторые из которых соединены кабелем. Компьютеры пронумеруем целыми числами от 1 до n. Известно, что любые два компьютера соединены кабелем непосредственно или через другие компьютеры.
Поликарп решил узнать топологию этой сети. Сетевая топология — это способ описания конфигурации сети, схема расположения и соединения сетевых устройств.
Поликарп знает три основные топологии сети: шина, кольцо и звезда. Шина — это топология, которая представляет собой общий кабель, к которому подсоединены все компьютеры. Кольцо — топология, в которой каждый компьютер соединен кабелем только с двумя другими. Звезда — это топология, в которой все компьютеры сети присоединены к единому центральному узлу.
Представим каждую из этих топологий сети в виде связного неориентированного графа. Под шиной будем понимать связный граф, являющийся единственным путем, то есть граф, в котором все вершины соединены с двумя другими, за исключением двух вершин, которые являются началом и концом пути. Под кольцом будем понимать связный граф, в котором все вершины соединены с двумя другими. Под звездой будем понимать связный граф, в котором выделена единственная центральная вершина, которая соединена со всеми остальными вершинами. Для лучшего понимания ознакомьтесь с рисунком.
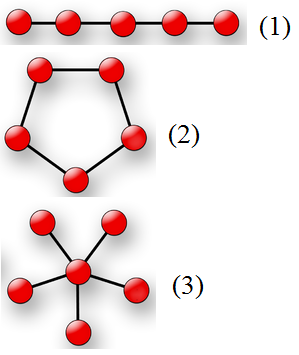 (1) — шина, (2) — кольцо, (3) — звезда
(1) — шина, (2) — кольцо, (3) — звезда Вам задан связный неориентированный граф, характеризующий компьютерную сеть корпорации, в которой работает Поликарп. Помогите ему узнать, к какой из данных топологий относится заданная компьютерная сеть. Если это невозможно определить, сообщите, что топология этой сети неизвестна.
В первой строке через пробел заданы два целых числа n и m (4 ≤ n ≤ 105; 3 ≤ m ≤ 105) — количество вершин и ребер в графе соответственно. Далее в m строках задано описание ребер графа. В i-той строке через пробел задана пара целых чисел xi, yi (1 ≤ xi, yi ≤ n) — номера вершин, которые соединяет i-ое ребро.
Гарантируется, что заданный граф является связным. Между любыми двумя вершинами существует не более одного ребра. Ни одно ребро не соединяет вершину саму с собой.
В единственную строку выведите название топологии сети, к которой относится заданный граф. Если ответом является шина, выведите «bus topology» (без кавычек), если ответом является кольцо, выведите «ring topology» (без кавычек), если ответом является звезда, выведите «star topology» (без кавычек). Если ни один из этих типов не подходит, выведите «unknown topology» (без кавычек).
4 3
1 2
2 3
3 4
bus topology
4 4
1 2
2 3
3 4
4 1
ring topology
4 3
1 2
1 3
1 4
star topology
4 4
1 2
2 3
3 1
1 4
unknown topology
| Название |
|---|




