| Codeforces Round 180 (Div. 1) |
|---|
| Закончено |
Белые мишки обнаружили гигантскую круглую плавающую льдину, а на ней были начертаны какие-то загадочные письмена. На льду выцарапано n линий. Каждая линия соединяет две точки на границе льдины (назовем эти точки конечными точками). Конечные точки пронумерованы по окружности как 1, 2, ..., 2n против часовой стрелки. Никакие две линии не имеют общей конечной точки.
Сейчас группа из 6 белых медведей (Алиса, Роберт, Каролина, Девид, Эвелина, Франк) собираются рыть берлоги в конечных точках. Каждому мишке хочется вырыть берлогу и жить в ней. Никакие два медведя не могут вырыть берлоги в одной и той же точке. Но вот Алиса и Роберт — суеверная парочка. Они верят, что эти линии начертали пришельцы (или люди, но для белых медведей это примерно одно и то же) — поэтому у линий есть определенная энергетическая сила. Следовательно, они хотят вырыть берлоги в двух концах, соединенных одной линией. То же самое относится к Каролине и Дэвиду, Эвелине и Франку.
Расстояние между двумя берлогами X и Y высчитывается как один плюс минимальное количество других берлог, мимо которых надо пройти, чтобы дойти от X до Y по границе льдины (конечные точки без берлог не берутся в расчет).
Чтобы все было по-честному, расстояние между тремя парочками должно быть одинаковым (то есть, расстояние между Алисой и Робертом, Каролиной и Дэвидом и расстояние между Эвелиной и Франком одинаковые).
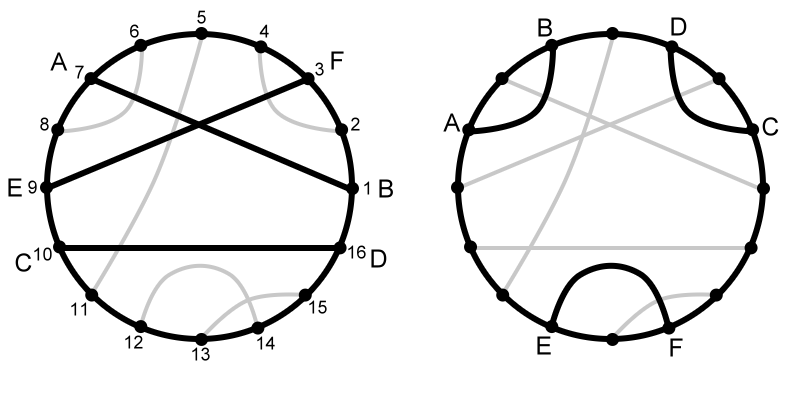
Рисунки ниже показывают две разных схемы, где конечные точки обозначаются точками на окружности. Схема слева не подходит. Несмотря на то, что каждая парочка (A и B, C и D, E и F) соединена линией, нарушено условие расстояния. Расстояние между A и B равняется 2 (можно дойти от A до B через F по часовой стрелке). Расстояние от E до F также равняется 2. Однако расстояние от C до D равняется 1 (можно пройти от C до D против часовой стрелки и не пройти мимо какой-либо другой берлоги). Справа показана верная схема. Все три пары имеют одинаковое расстояние 1.
Посчитайте, сколькими способами можно вырыть берлоги по данным требованиям. Два способа считаются одинаковыми, если использован один и тот же набор 6 конечных точек.
Первая строка содержит целое число n (3 ≤ n ≤ 105) — количество линий.
Каждая из следующих n строк содержит два целых числа ai, bi (1 ≤ ai, bi ≤ 2n), означающих, что на льду начертана линия, соединяющая ai–тую и bi–тую конечные точки.
Гарантируется, что никакая конечная точка не принадлежит двум разным линиям.
Выведите количество способов вырыть берлоги.
Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d.
4
5 4
1 2
6 7
8 3
2
8
1 7
2 4
3 9
5 11
6 8
10 16
13 15
14 12
6
Второй пример описывает рисунок из условия задачи.
| Название |
|---|




