| Codeforces Round 185 (Div. 1) |
|---|
| Закончено |
Рейнбоу выстроил h ячеек в ряд и пронумеровал их от 1 до h слева направо. В n из этих ячеек находится сокровище. Будем называть каждую из этих n ячеек «ячейка с сокровищами». «Ячейка с сокровищами» номер i — это ai-ая ячейка, в ней лежат сокровища на ci долларов.
Сейчас Фреда встала в первую ячейку. В любой момент она может пройти k ячеек вперед или вернуться в первую ячейку. Это значит, что Фреда может дойти до 1-ой, (k + 1)-ой, (2·k + 1)-ой, (3·k + 1)-ой ячеек и так далее.
Рейнбоу дала Фреде m операций. Каждая операция относится к одному из следующих трех типов:
- Добавить способ перемещения x: в любой момент времени можно также пройти на x ячеек вперед. Например, в самом начале у Фреды есть только один способ перемещения k. Если в какой-то момент времени у Фреды есть способы перемещения a1, a2, ..., ar, то она может дойти до любой ячейки вида
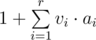 , где vi — некоторое целое неотрицательное число.
, где vi — некоторое целое неотрицательное число. - Уменьшить цену сокровища в x-ой «ячейке с сокровищами» на y долларов. Иными словами, выполнить присвоение cx = cx - y.
- Узнать стоимость самого ценного сокровища среди ячеек, до которых может дойти Фреда. Если Фреда не может дойти ни до одной ячейки с сокровищами, то считается, что стоимость самого ценного сокровища в таком случае равна 0 и дальше ничего не происходит. Иначе, Фреда забирает самое ценное сокровище из соответствующей ячейки. Если существует несколько «ячеек с сокровищами», которые содержат самое ценное сокровище, то нужно выбрать ту, номер которой минимален (такая ячейка не обязательно имеет минимальный номер, потому что нумерации ячеек и «ячеек с сокровищами» независимы). После этой операции количество ячеек, в которых содержится сокровище, становится на единицу меньше.
Фреда как программист просит Вас написать программу, которая выполнит каждую операцию.
Первая строка содержит четыре целых числа: h (1 ≤ h ≤ 1018), n, m (1 ≤ n, m ≤ 105) и k (1 ≤ k ≤ 104).
Каждая из следующих n строк содержит два целых числа: ai (1 ≤ ai ≤ h), ci (1 ≤ ci ≤ 109). Это означает, что i-ая «ячейка с сокровищами» — это ai-ая ячейка и в ней лежит сокровище на ci долларов. Все ai различны.
Каждая из следующих m строк записана в одном из следующих трех форматов:
- «1 x» — операция типа 1, 1 ≤ x ≤ h;
- «2 x y» — операция типа 2, 1 ≤ x ≤ n, 0 ≤ y < cx;
- «3» — операция типа 3.
Максимальное количество операций типа 1 — 20. Гарантируется, что в любой момент стоимость сокровища в любой ячейке с сокровищем положительна. Гарантируется, что все операции корректны (никакая операция не может уменьшить стоимость уже взятого сокровища).
Пожалуйста, не используйте спецификатор %lld, для чтения 64-битных чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d.
Для каждой операции типа 3, выведите целое число, указывающее на ценность (в долларах) самого ценного сокровища среди «ячеек c сокровищами», которые Фреда может достать. Если такого сокровища нет, выведите 0.
10 3 5 2
5 50
7 60
8 100
2 2 5
3
1 3
3
3
55
100
50
В примере дано 10 ячеек и 3 «ячейки с сокровищами». Первая — это ячейка 5, в ней лежит сокровище на 50 долларов. Вторая — это ячейка 7, в ней лежит сокровище на 60 долларов. Третья — это ячейка 8, в ней лежит сокровище на 100 долларов.
Сначала Фреда может дотянуться только до ячеек 1, 3, 5, 7 и 9. Первая операция уменьшает стоимость в долларах второй «ячейки с сокровищами» с 60 до 55. После этого самое ценное сокровище среди доступных ей «ячеек с сокровищами» — это max(50, 55) = 55. После третьей операции она может двигаться на 3 ячейки вперед с каждым шагом, таким образом она может достигнуть ячеек 1, 3, 4, 5, 6, 7, 8, 9, 10. Значит, четвертая операция забирает сокровище стоимостью 100 долларов.
Обратите внимание, что она забрала сокровище стоимостью 55 и 100 долларов, следовательно, ответ последней операцией она забирает сокровище стоимостью 50 долларов.
| Название |
|---|




