| ABBYY Cup 3.0 |
|---|
| Закончено |
Умный Бобер следит за своим внешним видом, а особое внимание уделяет обуви, потому имеет огромное количество пар кроссовок от самых известных лесных брендов. Он старается аккуратно складывать свои ботинки, чтобы каждая пара стояла рядышком. Но к концу недели из-за достаточно активного образа жизни в его гардеробной образуется беспорядок.
Умный Бобер из ABBYY является не только самым эрудированным бобром в округе, но еще и самым хозяйственным. Например, по понедельникам Умный Бобер устраивает генеральную уборку в своем жилище.
Настало утро понедельника. Тратить на уборку весь день Умный Бобер не хочет, да еще и дел много, в тренажерный зал успеть нужно, потому желает прибраться как можно скорее. И вот полы вымыты, пыль вытерта — время прибраться в гардеробной. Но как только Умный Бобер вошел в гардеробную — все планы на день были вмиг разрушены: там царил полный хаос и казалось, что невозможно справиться даже за неделю. Обнадежьте нашего героя: подскажите ему, какое минимальное количество ботинок должно изменить свое положение, чтобы в гардеробной наступил порядок.
Гардеробная имеет прямоугольную форму и разделена на n × m равных квадратов, причем в каждом квадрате лежит ровно по одному ботинку. Каждая пара обуви пронумерована уникальным числом от 1 до 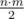 . Квадрат с координатами (i, j) содержит целое число — номер пары, которой принадлежит ботинок, лежащий в нем. Умный Бобер считает, что в гардеробной порядок, только когда каждая пара кроссовок лежит рядом. Будем считать, что пара кроссовок в квадратах (i1, j1) и (i2, j2) лежит рядом, если |i1 - i2| + |j1 - j2| = 1.
. Квадрат с координатами (i, j) содержит целое число — номер пары, которой принадлежит ботинок, лежащий в нем. Умный Бобер считает, что в гардеробной порядок, только когда каждая пара кроссовок лежит рядом. Будем считать, что пара кроссовок в квадратах (i1, j1) и (i2, j2) лежит рядом, если |i1 - i2| + |j1 - j2| = 1.
Первая строка содержит два целых числа n и m, разделенных пробелом. Они соответствуют размеру гардеробной. Следующие n строк содержат по m целых чисел, разделенных пробелами. Эти числа описывают гардеробную. Каждое число соответствует одному из кроссовок.
Гарантируется, что:
- n·m будет четно.
- Все числа, соответствующие номерам пар кроссовок в гардеробной, будут лежать в пределах от 1 до
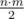 .
. - Каждое из чисел от 1 до
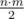 будет встречаться ровно дважды.
будет встречаться ровно дважды.
Ограничения на входные данные для получения 30 баллов (подзадача C1):
- 2 ≤ n, m ≤ 8.
Ограничения на входные данные для получения 100 баллов (подзадачи C1+C2):
- 2 ≤ n, m ≤ 80.
Выведите ровно одно целое число — минимальное число кроссовок, которые должны поменять свое местоположение.
2 3
1 1 2
2 3 3
2
3 4
1 3 2 6
2 1 5 6
4 4 5 3
4
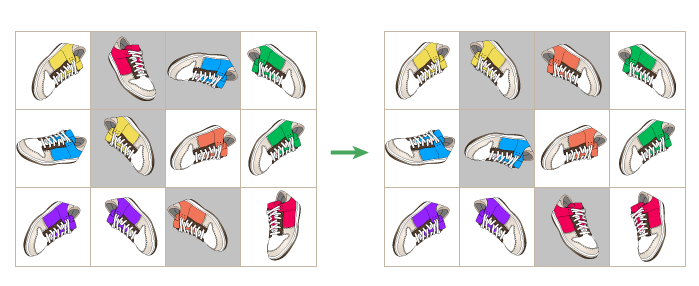 Второй пример.
Второй пример. | Название |
|---|




