| Codeforces Round 190 (Div. 1) |
|---|
| Закончено |
Лиса Ciel зашла в парк аттракционов. И вот, она в очереди на колесо обозрения. В очереди стоит n людей (хотя нет, скорее лис): мы будем считать, что первая лиса стоит в начале очереди, а n-ая лиса стоит в хвосте очереди.
Всего имеется k гондол, мы распределяем лис по гондолам следующим образом:
- Когда подплывает первая гондола, q1 лис переходят из начала очереди в подплывшую гондолу.
- Затем, когда подплывает вторая гондола, q2 лис из начала оставшейся очереди переходит в эту гондолу.
...
- Оставшиеся qk лис идут с последнюю (k-ую) гондолу.
Обратите внимание, что числа q1, q2, ..., qk должны быть положительные. Из условия следует, что 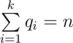 и qi > 0.
и qi > 0.
Вы знаете как лисам не хочется задерживаться в гондолах с незнакомцами. Итак, Ваша задача — найти оптимальный способ размещения (то есть определить оптимальную последовательность q), чтобы угодить всем. Для каждой пары лис i и j задано значение uij, обозначающее степень незнакомости. Можете считать, что uij = uji для всех i, j (1 ≤ i, j ≤ n) и что uii = 0 для всех i (1 ≤ i ≤ n). Тогда значение незнакомости в гондоле определяется как сумма значений незнакомости между всеми парами лис, которые находятся в этой гондоле. Общее значение незнакомости определяется как сумма значений незнакомости по всем гондолам.
Помогите лисе Ciel найти минимальное возможное значение общей незнакомости при некотором оптимальном распределении лис по гондолам.
В первой строке даны два целых числа n и k (1 ≤ n ≤ 4000 and 1 ≤ k ≤ min(n, 800)) — количество лис в очереди и количество гондол. В следующих n строках записано по n целых чисел — матрица u, (0 ≤ uij ≤ 9, uij = uji и uii = 0).
Пожалуйста, используйте методы быстрого чтения (например, для Java используйте BufferedReader вместо Scanner).
Выведите целое число — минимальное возможное значение общей незнакомости.
5 2
0 0 1 1 1
0 0 1 1 1
1 1 0 0 0
1 1 0 0 0
1 1 0 0 0
0
8 3
0 1 1 1 1 1 1 1
1 0 1 1 1 1 1 1
1 1 0 1 1 1 1 1
1 1 1 0 1 1 1 1
1 1 1 1 0 1 1 1
1 1 1 1 1 0 1 1
1 1 1 1 1 1 0 1
1 1 1 1 1 1 1 0
7
3 2
0 2 0
2 0 3
0 3 0
2
В первом примере можно распределить лис вот так: {1, 2} идут в одну гондолу, {3, 4, 5} идут в другую гондолу.
Во втором примере оптимальное распределение таково: {1, 2, 3} | {4, 5, 6} | {7, 8}.
| Название |
|---|




