Вам даны n прямоугольников, пронумерованных от 1 до n. Углы прямоугольников имеют целые координаты, а стороны прямоугольников параллельны осям Ox и Oy. Прямоугольники могут касаться, но никогда не пересекаются (иными словами, не существует точки, принадлежащей внутренней области более чем одного прямоугольника).
Ваша задача определить, существует ли непустое подмножество данных прямоугольников, которые образуют квадрат. Другими словами, определите, существует ли такое подмножество данных прямоугольников, и такой квадрат, что любая точка, которая принадлежит внутренней области или границе квадрата принадлежит внутренней области или границе хотя бы одного из прямоугольников в подмножестве, а любая точка, которая принадлежит внутренней области или границе хотя бы одного из прямоугольников этого подмножества также принадлежит квадрату.
Первая строка содержит целое число n (1 ≤ n ≤ 105) — количество прямоугольников. Каждая из следующих n строк содержит описание прямоугольника, где i-ая строка описывает прямоугольник с номером i. Описание прямоугольника состоит из четырех целых чисел: x1, y1, x2, y2 — координат левого нижнего и правого верхнего углов прямоугольника (0 ≤ x1 < x2 ≤ 3000, 0 ≤ y1 < y2 ≤ 3000).
Никакие два прямоугольника не пересекаются (не существует точки, принадлежащей внутренней области более чем одного прямоугольника).
Если такое подмножество существует, выведите «YES» (без кавычек) в первой строке, а затем на этой же строке число k — количество прямоугольников в подмножестве. На второй строке выведите k чисел — номера прямоугольников в подмножестве в любом порядке. Если существует более одного такого подмножества, выведите любое. Если такого подмножества не существует, выведите «NO» (без кавычек).
9
0 0 1 9
1 0 9 1
1 8 9 9
8 1 9 8
2 2 3 6
3 2 7 3
2 6 7 7
5 3 7 6
3 3 5 6
YES 5
5 6 7 8 9
4
0 0 1 9
1 0 9 1
1 8 9 9
8 1 9 8
NO
Первый тест представлен на картинке:
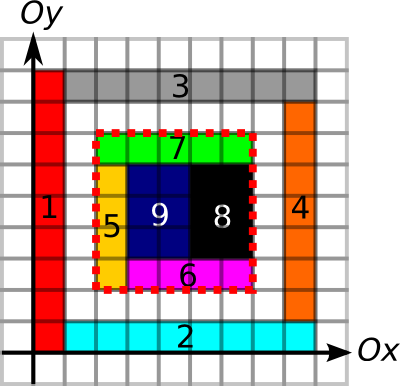
Обратите внимание, что прямоугольники 6, 8, и 9 тоже образуют квадрат, и будут приняты как ответ.
Второй тест представлен на картинке:
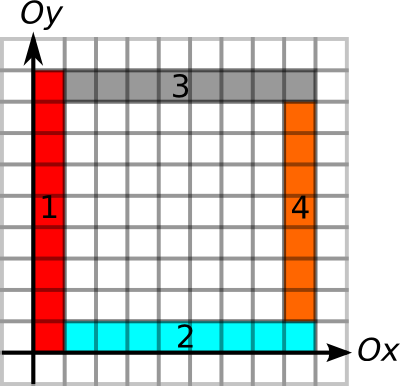
| Название |
|---|




