Некоторое количество небоскребов x были построены в один ряд. Целое число x выбрано случайно равновероятно среди всех целых чисел от 2 до 314! (314! — это факториал числа 314 — очень большое число). Высота каждого небоскреба была выбрана случайно и независимо, для каждого небоскреба высота i (i — целое число, i > 0) была выбрана с вероятностью 2^- i. В небоскребе с высотой i этажи пронумерованы от 0 до i - 1.

Чтобы оптимизировать время, которое нужно для перемещения между небоскребами, было построено несколько зиплайнов (металлических тросов, по которым можно передвигаться) между небоскребами. Зиплайн всегда связывает i-ый этаж одного небоскреба с i-ым этажом другого небоскреба, и есть тогда и только тогда, когда между соответствующими небоскребами нет ни одного небоскреба, у которого есть i-ый этаж.

Алиса и Боб решили посчитать количество небоскребов.

Алиса хочет знать точное количество небоскребов. Она начинает с самого левого небоскреба, с значением счетчика равным 1. Затем она идет вправо, и для каждого небоскреба, который она встречает, прибавляет 1 к счетчику. Она продолжает пока не доходит до самого правого небоскреба.

Боб очень нетерпелив и хочет закончить подсчет как можно скорее. Он начинает с самого левого небоскреба с значением счетчика равным 1, но передвигается между небоскребами по зиплайнам. На каждом шагу Боб использует для передвижения направо самый высокий зиплайн, который ему доступен, на этаже не выше, чем h — использовать зиплайны выше ему не позволяет боязнь высоты. Когда Боб использует зиплайн, он едет так быстро, что не способен оценить, насколько большое было расстояние между небоскребами. Поэтому он просто прибавляет 2ⁱ к счетчику, где i — это этаж, на котором был зиплайн. Боб продолжает передвигаться, пока не оказывается в самом правом небоскребе.

Рассмотрим пример. Всего есть 6 небоскребов, с высотами 1, 4, 3, 4, 1, 2 слева направо. Допустим h = 2. Алиса начинает с значением счетчика 1 и затем добавляет к нему 1 пять раз, получив в итоге 6. Боб также начинает со значением счетчика 1, затем добавляет 1, 4, 4, и 2, получив в итоге 12. Обратите внимание, что Боб не всегда использует самый высокий доступный зиплайн из-за боязни высоты (h = 2).

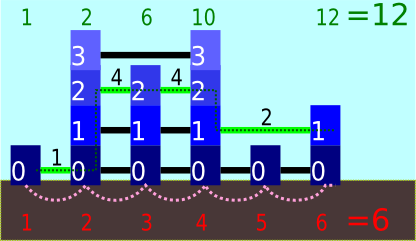
Значения счетчика Боба в разное время показано вверху, а Алисы — внизу. На рисунке присутствуют все зиплайны. Путь Боба показан пунктирной зеленой линией, а Алисы — пунктирной розовой. Возле этажей подписаны их номера, а возле зиплайнов, которые использовал Боб — значение, которое он добавил к счетчику, передвигаясь по ним.

Когда Алиса и Боб встретились в самом правом небоскребе, они сравнили значения счетчиков. Вам будет дано значение, которое в итоге получила Алиса или Боб. Ваша задача определить ожидаемое значение счетчика второго персонажа.