| Codeforces Round 195 (Div. 2) |
|---|
| Закончено |
У медведя Василия есть два любимых целых числа n и k, а также карандаш. Кроме того, у него есть k банок с акварельными красками различных цветов. Все банки пронумерованы некоторым образом от 1 до k включительно. В банке с номером i находится краска i-ого цвета.
Изначально на координатной плоскости медведь нарисовал карандашом четыре отрезка. Все они имеют в качестве конца точку (0, 0), а качестве начала они имеют следующие точки: (0, 2n), (0, - 2n), (2n, 0), ( - 2n, 0). Далее для каждого i = 1, 2, ..., n медведь нарисовал два квадрата. Первый квадрат имеет следующие координаты вершин: (2i, 0), ( - 2i, 0), (0, - 2i), (0, 2i). Второй квадрат имеет следующие координаты вершин: ( - 2i - 1, - 2i - 1), ( - 2i - 1, 2i - 1), (2i - 1, - 2i - 1), (2i - 1, 2i - 1). После всего этого медведь нарисовал еще один квадрат: (1, 0), ( - 1, 0), (0, - 1), (0, 1). Все точки, упомянутые выше, образуют множество точек A.

Пример полученного рисунка при n = 0
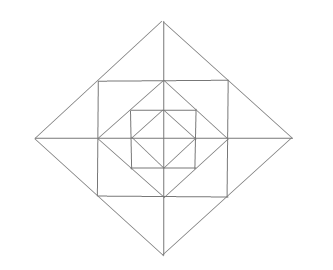
Пример полученного рисунка при n = 2
Медведь решил покрасить полученный рисунок за k ходов, i-ый ход состоит из следующих этапов:
- Медведь выбирает 3 различных точки в множестве А так, чтобы между любой парой выбранных точек на рисунке существовал отрезок. Внутри области, ограниченной выбранными точками и отрезками между ними, не должно быть точек, уже покрашенных некоторой акварельной краской.
- Медведь закрашивает в i-ый цвет область, ограниченную выбранными точками и отрезками.
Отметим, что после k-ого хода некоторые части рисунка могут остаться непокрашенными.
Медведь попросил Вас определить количество различных способов покраски его рисунка. Способом покраски Василий называет последовательность трехэлементных множеств точек, выбранных им на каждом из ходов. Две последовательности множеств считаются различными, если существует такое число i (1 ≤ i ≤ k), что i-ые члены этих последовательностей не совпадают как множества. Так как искомое количество способов покраски может быть довольно большим, требуется найти лишь остаток от деления его на число 1000000007 (109 + 7).
Первая строка содержит два целых числа n и k, записанные через пробел (0 ≤ n, k ≤ 200).
Выведите ровно одно число — ответ на задачу по модулю 1000000007 (109 + 7).
0 0
1
0 1
8
0 2
32
1 1
32
| Название |
|---|




