| Codeforces Round 203 (Div. 2) |
|---|
| Закончено |
Валера проводит эксперименты с алгоритмами поиска кратчайших путей. Недавно он изучил алгоритм Флойда, сегодня Валера решил поэкспериментировать именно с ним.
Валера уже написал код, который посчитает ему кратчайшие расстояния между всеми парами вершин в неориентированном связном графе из n вершин и m ребер, не содержащем петли и кратные ребра. Также Валера решил часть вершин пометить, а именно он пометил ровно k вершин a1, a2, ..., ak.
Ниже приведена реализация его алгоритма.
ans[i][j] // кратчайшее расстояние для пары вершин i, j
a[i] // помеченные Валерой вершины
for(i = 1; i <= n; i++) {
for(j = 1; j <= n; j++) {
if (i == j)
ans[i][j] = 0;
else
ans[i][j] = INF; //INF — очень большое число
}
}
for(i = 1; i <= m; i++) {
считать пару вершин u, v, между которыми есть неориентированное ребро;
ans[u][v] = 1;
ans[v][u] = 1;
}
for (i = 1; i <= k; i++) {
v = a[i];
for(j = 1; j <= n; j++)
for(r = 1; r <= n; r++)
ans[j][r] = min(ans[j][r], ans[j][v] + ans[v][r]);
}
Валера понял, что его код неверный. Помогите Валере, найдите для заданного набора помеченных вершин a1, a2, ..., ak такой неориентированный связный граф, состоящий из n вершин и m ребер, для которого код Валеры хотя бы для одной из пар вершин (i, j) посчитает неверное кратчайшее расстояние. Валера очень хочет, чтобы найденный граф не содержал петли и кратные ребра. Если же такого графа не существует, выведите -1.
В первой строке входных данных записаны три целых числа n, m, k (3 ≤ n ≤ 300, 2 ≤ k ≤ n , 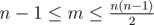 ) — количество вершин, количество ребер, и количество помеченных вершин.
) — количество вершин, количество ребер, и количество помеченных вершин.
Во второй строке входных данных записаны k целых чисел через пробел a1, a2, ... ak (1 ≤ ai ≤ n) — номера помеченных вершин. Гарантируется, все числа ai различны.
Если требуемого графа не существует выведите в единственной строке -1. Иначе выведите m строк по два целых числа u, v — описание ребер искомого Валерой графа.
3 2 2
1 2
1 3
2 3
3 3 2
1 2
-1
| Название |
|---|




