| Codeforces Round 218 (Div. 2) |
|---|
| Закончено |
В данной задаче речь пойдет только о массивах, все элементы которых равны 1 и/или 2.
Массив a называется k-периодичным, если его длина делится нацело на k, и существует такой массив b длины k, что a представляет собой записанный ровно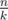 
раз подряд массив b. Иными словами, массив a является k-периодичным, если он имеет период длины k.
Например, любой массив является n-периодичным, где n — длина массива. Массив [2, 1, 2, 1, 2, 1] является одновременно 2-периодичным и 6-периодичным, а массив [1, 2, 1, 1, 2, 1, 1, 2, 1] является одновременно 3-периодичным и 9-периодичным.
Для заданного массива a, состоящего только из единиц и двоек, найдите наименьшее количество элементов, которые необходимо изменить, чтобы он стал k-периодичным. Если массив уже является k-периодичным, то искомое значение равно 0.
В первой строке входных данных содержится пара целых положительных чисел n, k (1 ≤ k ≤ n ≤ 100), где n — длина массива, а значение k делит нацело n. Вторая строка содержит последовательность элементов заданного массива a1, a2, ..., an (1 ≤ ai ≤ 2), ai — i-й элемент массива.
Выведите наименьшее количество элементов массива, которые надо изменить, чтобы он стал k-периодическим. Если массив уже является k-периодичным, то выведите 0.
6 2
2 1 2 2 2 1
1
8 4
1 1 2 1 1 1 2 1
0
9 3
2 1 1 1 2 1 1 1 2
3
В первом примере достаточно заменить четвертый элемент с 2 на 1, тогда массив примет вид [2, 1, 2, 1, 2, 1].
Во втором примере заданный массив уже 4-периодичный.
В третьем примере достаточно каждое вхождение двойки заменить на единицу. В этом случае массив примет вид [1, 1, 1, 1, 1, 1, 1, 1, 1] — этот массив одновременно 1-, 3- и 9-периодичный.
