| Codeforces Round 218 (Div. 2) |
|---|
| Закончено |
В Берляндии неспокойно — упавшие цены на грязь подорвали бюджет этой страны. Ведь все знают, что Берляндия — крупнейший в мире экспортер грязи!
Президенту Берляндии нелегко далось решение, что из n станций метрополитена столицы необходимо оставить только k.
Станции метрополитена расположены на прямой одна за другой, поезда курсируют проезжая станции последовательно. Удобно считать, что станции расположены на оси Ox, i-ая станция расположена в точке с координатой xi. В таком случае расстояние между станциями i и j вычисляется по простой формуле |xi - xj|.
В настоящий момент министерство транспорта решает, какие из станций следует закрыть, а какие оставить. Очевидно, что жители столицы без восторга отнесутся к этой реформе, поэтому решено представить ее с выгодной стороны. Министерство транспорта хочет выбрать такие k станций, чтобы минимизировать среднее время проезда в метро!
Считая, что скорость движения поезда постоянна (константа), среднее время проезда в метро вычисляется как сумма попарных расстояний между станциями, деленная на количество пар (оно равно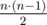 
) и деленная на скорость движения поезда.
Помогите министру транспорта решить эту непростую задачу. Напишите программу, которая по заданным положениям станций выбирает такие k станций, что среднее время проезда в метро минимизируется.
В первой строке входных данных записано целое число n (3 ≤ n ≤ 3·105) — количество станций до реформы. Вторая строка содержит координаты станций x1, x2, ..., xn ( - 108 ≤ xi ≤ 108). Третья строка содержит целое число k (2 ≤ k ≤ n - 1) — количество станций после реформы.
Координаты станций не обязательно отсортированы. Все координаты станций различны.
Выведите последовательность из k различных целых чисел t1, t2, ..., tk (1 ≤ tj ≤ n) — номера станций, которые следует оставить после реформы, в произвольном порядке. Считайте, что станции пронумерованы от 1 до n в том порядке, как они заданы во входных данных. Выведенный набор станций должен иметь наименьшее возможное среднее время проезда среди всех возможных способов выбрать k станций. Если таких способов несколько, то разрешается вывести любой из них.
3
1 100 101
2
2 3
В тестовом примере оптимальным решением является решение удалить станцию в координате x = 1. В таком случае полученное среднее время проезда будет равно 1.
