| Codeforces Round 219 (Div. 1) |
|---|
| Закончено |
Дано множество из S точек на плоскости. Это множество не включает начала координат O(0, 0), а для каждых двух различных точек A и B из множества треугольник OAB имеет строго положительную площадь.
Рассмотрим множество пар точек (P1, P2), (P3, P4), ..., (P2k - 1, P2k). Назовем такое множество хорошим тогда и только тогда, когда:
- k ≥ 2.
- Все Pi различные и каждая точка Pi является элементом S.
- Для любых двух пар (P2i - 1, P2i) и (P2j - 1, P2j) описанные окружности треугольников OP2i - 1P2j - 1 и OP2iP2j имеют единственную общую точку, и описанные окружности треугольников OP2i - 1P2j и OP2iP2j - 1 имеют единственную общую точку.
Вычислите количество хороших множеств пар точек по модулю 1000000007 (109 + 7).
В первой строке записано единственное целое число n (1 ≤ n ≤ 1000) — количество точек в S. Каждая из следующих n строк содержит четыре целых числа ai, bi, ci, di (0 ≤ |ai|, |ci| ≤ 50; 1 ≤ bi, di ≤ 50; (ai, ci) ≠ (0, 0)). Эти целые числа обозначают точку 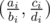 .
.
Никакие две точки не совпадают.
Выведите единственное целое число — ответ на задачу по модулю 1000000007 (109 + 7).
10
-46 46 0 36
0 20 -24 48
-50 50 -49 49
-20 50 8 40
-15 30 14 28
4 10 -4 5
6 15 8 10
-20 50 -3 15
4 34 -16 34
16 34 2 17
2
10
30 30 -26 26
0 15 -36 36
-28 28 -34 34
10 10 0 4
-8 20 40 50
9 45 12 30
6 15 7 35
36 45 -8 20
-16 34 -4 34
4 34 8 17
4
10
0 20 38 38
-30 30 -13 13
-11 11 16 16
30 30 0 37
6 30 -4 10
6 15 12 15
-4 5 -10 25
-16 20 4 10
8 17 -2 17
16 34 2 17
10
| Название |
|---|




