| Codeforces Round 228 (Div. 1) |
|---|
| Закончено |
Лиса Сиель изучает теорию чисел.
Она считает, что непустое множество S, состоящее из неотрицательных целых чисел, является идеальным тогда и только тогда, когда для любых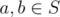 
(a может равняться b), 
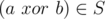. Где операция xor означает операцию исключающего ИЛИ (http://ru.wikipedia.org/wiki/Сложение_по_модулю_2).
Пожалуйста, вычислите количество идеальных множеств, состоящих из целых чисел, не превосходящих k. Ответ может получиться достаточно большим, поэтому выведите его по модулю 1000000007 (109 + 7).
В первой строке записано целое число k (0 ≤ k ≤ 109).
Выведите единственное целое число — количество искомых множеств по модулю 1000000007 (109 + 7).
1
2
2
3
3
5
4
6
В первом тестовом примере существует 2 таких множества: {0} и {0, 1}. Обратите внимание, что {1} не является идеальным множеством, так как 1 xor 1 = 0 и {1} не содержит нулей.
В четвертом примере существует 6 таких множеств: {0}, {0, 1}, {0, 2}, {0, 3}, {0, 4} и {0, 1, 2, 3}.
