| Rockethon 2014 |
|---|
| Закончено |
Задача состоит из трех подзадач: за решение подзадачи F1 вы получите 8 баллов, за решение подзадачи F2 вы получите 15 баллов, за решение подзадачи F3 вы получите 10 баллов.
Манао разработал модель, предсказывающую цены акций некоторой компании на протяжении следующих n дней. Теперь он хочет получить максимальную прибыль, используя результаты этой модели. К сожалению, торговый счет Манао имеет следующие ограничения:
- В любой момент времени, Манао может иметь либо 0, либо 1 акцию.
- Продажа или покупка акций может быть произведена лишь раз в день.
- В течение следующих n дней ему позволено произвести покупку акций не более k раз.
В этой задаче мы будем называть сделкой процесс покупки акции в некоторый день i и ее сохранения до дня j > i, в который акция будет продана. Предыдущие ограничения можно записать следующим образом: Манао разрешено сделать не более k непересекающихся сделок на протяжении n дней, для которых модель Манао предсказала цены акций.
Хотя имея возможность держать на руках более одной акции или производить более k сделок, Манао и смог бы получить больше прибыли, у него все равно есть шанс разбогатеть, учитывая что его модель делает точные предсказания. Например, зная наперед все цены, Манао может дождаться дня с низкой ценой акций, купить одну акцию и ждать дня с высокой ценой, в который он ее продаст, и повторять это k раз в течение n дней.
Тем не менее, для Манао недостаточно иметь просто хороший алгоритм купли-продажи, он хочет выработать оптимальную стратегию для максимизации прибыли при данных ограничениях. Помогите ему достичь этой цели, написав программу, которая определит, когда покупать и продавать акции, чтобы достичь максимально возможной прибыли.
В первой строке записаны два разделенных пробелом целых числа n и k 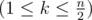 . Далее следует n строк, i-ая из которых содержит одно целое число pi (0 ≤ pi ≤ 1012) — цену, за которую можно купить или продать акции в i-ый день рассматриваемого процесса.
. Далее следует n строк, i-ая из которых содержит одно целое число pi (0 ≤ pi ≤ 1012) — цену, за которую можно купить или продать акции в i-ый день рассматриваемого процесса.
Задача состоит из трех подзадач, которые отличаются друг от друга ограничениями на входные данные. За решение каждой подзадачи вы получите определенное количество баллов. Описание подзадач следует ниже.
- В подзадаче F1 (8 баллов) ограничение на n следующее: 1 ≤ n ≤ 3000.
- В подзадаче F2 (15 баллов) ограничение на n следующее: 1 ≤ n ≤ 100000.
- В подзадаче F3 (10 баллов) ограничение на n следующее: 1 ≤ n ≤ 4000000.
Выведите единственное целое число — максимальное количество прибыли, которое Манао может извлечь, если перед первым из n рассматриваемых дней у него на руках нет акций, в любой момент времени он владеет 0 или 1 акцией и производит не более k непересекающихся сделок.
10 2
2
7
3
9
8
7
9
7
1
9
15
10 5
2
7
3
9
8
7
9
7
1
9
21
В первом примере наилучшей сделкой является купить акцию по цене 1 на девятый день и продать по цене 9 на десятый день, а следующей наилучшей сделкой является покупка акции по цене 2 на первый день и продажа этой акции по цене 9 на четвертый день. Так как эти две сделки не пересекаются, оптимальной стратегией является совершить обе. Таким образом, его план купли-продажи выглядит следующим образом:
2 | 7 | 3 | 9 | 8 | 7 | 9 | 7 | 1 | 9
buy | | | sell | | | | | buy | sell
Таким образом, суммарная прибыль (9 - 2) + (9 - 1) = 15.
Во втором примере, хоть у Манао и есть возможность совершить вплоть до 5 сделок, только 4 из них могут быть прибыльными. Оптимальным решением является покупать и продавать в следующие дни:
2 | 7 | 3 | 9 | 8 | 7 | 9 | 7 | 1 | 9
buy | sell | buy | sell | | buy | sell | | buy | sell
Суммарная прибыль от такой стратегии — (7 - 2) + (9 - 3) + (9 - 7) + (9 - 1) = 21.
| Название |
|---|




