| Codeforces Round 238 (Div. 2) |
|---|
| Закончено |
Маленький Крис принимает участие в соревновании по нарезке графов. В этом он профессионал. Настал час устроить серьезную проверку его способностям.
Крису дан простой неориентированный связный граф, который состоит из n вершин (пронумерованных от 1 до n) и m ребер. Задача Криса состоит в том, чтобы разрезать заданный граф на пути длины 2. Формально, Крису надо разбить все ребра графа на пары так, чтобы в каждой паре ребра были смежные (инцидентны некоторой общей вершине) и каждое ребро содержалось ровно в одной паре.
Например, ниже приведен рисунок, который показывает, как Крис может разрезать граф. Первый тестовый пример содержит описание этого графа.

Вам дана возможность посоревноваться с Крисом. Найдите способ разрезать данный граф или же определите, что это невозможно!
В первой строке входных данных даны два целых числа через пробел, n и m (1 ≤ n, m ≤ 105), количество вершин и ребер в графе, соответственно. Следующие m строк содержат описание ребер графа. В i-й строке записаны два целых числа через пробел ai и bi (1 ≤ ai, bi ≤ n; ai ≠ bi), номера вершин, соединенных i-м ребром.
Гарантируется, что данный граф простой (не содержит петель и мультиребер) и связный.
Обратите внимание: входные и выходные данные имеют очень большой размер, не стоит использовать медленные методы ввода и вывода данных вашего языка программирования. Например, в языке C++ не стоит использовать потоки ввода и вывода (cin, cout).
Если данный граф возможно разрезать на пути длины 2, выведите 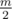 строк. В i-й строке выведите три целых числа через пробел, xi, yi и zi, описание i-го пути. Граф должен содержать этот путь, то есть в графе должны быть ребра (xi, yi) и (yi, zi). Каждое ребро должно присутствовать ровно в одном пути длины 2. Если есть несколько вариантов решения, выведите любой из них.
строк. В i-й строке выведите три целых числа через пробел, xi, yi и zi, описание i-го пути. Граф должен содержать этот путь, то есть в графе должны быть ребра (xi, yi) и (yi, zi). Каждое ребро должно присутствовать ровно в одном пути длины 2. Если есть несколько вариантов решения, выведите любой из них.
Если данный граф разрезать невозможно, выведите "No solution" (без кавычек).
8 12
1 2
2 3
3 4
4 1
1 3
2 4
3 5
3 6
5 6
6 7
6 8
7 8
1 2 4
1 3 2
1 4 3
5 3 6
5 6 8
6 7 8
3 3
1 2
2 3
3 1
No solution
3 2
1 2
2 3
1 2 3
| Название |
|---|




