| Codeforces Round 249 (Div. 2) |
|---|
| Закончено |
В этой задаче вам придется иметь дело с графом-сеткой размера n × m. Вершины этого графа — это узлы сетки n × m. Ребра этого графа — это все стороны и диагонали единичных квадратов сетки.
На рисунке ниже изображен граф размера 3 × 5. Черные линии изображают ребра графа, цветные кружочки изображают вершины графа. Вершины графа на рисунке раскрашены не просто так, раскраска является корректной вершинной раскраской графа размера 3 × 5 в четыре цвета. Раскраска называется корректной тогда и только тогда, когда каждая вершина покрашена, и никакие две вершины, соединенные ребром, не покрашены в один и тот же цвет.
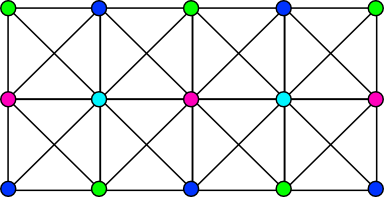
Задан размер графа-сетки n × m, а также цвета некоторых его вершин. Найдите хотя бы один способ раскрасить вершины, цвета которых не заданы, в четыре цвета, чтобы итоговая раскраска являлась корректной вершинной раскраской. Если такого способа не существует, сообщите об этом.
В первой строке записаны два целых числа n и m (2 ≤ n, m ≤ 1000). В каждой из следующих n строк записано по m символов — заданный граф. Каждый символ — это один из символов: «0», «1», «2», «3», «4». Символ «0» обозначает, что цвет соответствующей вершины графа не задан, остальные символы обозначают, что вершина покрашена в заданный цвет.
Считайте, что цвета пронумерованы от 1 до 4.
Если описанного способа не существует, в единственной строке выведите 0. Иначе выведите покрашенный граф размера n × m. Выводите граф в таком же формате, в котором он задан во входных данных.
Если существует несколько правильных ответов, разрешается вывести любой.
3 5
10101
00020
01000
13131
42424
31313
2 2
00
00
12
34
2 2
11
00
0
В первом тестовом примере ответ совпадает с картинкой из условия (1 — зеленый цвет, 2 — голубой, 3 — синий, 4 — розовый).
На второй тестовый пример существует ровно 4! ответов, любой из них считается правильным.
В третьем тестовом примере в изначальной раскраске две вершины одного цвета соединены ребром. Значит нельзя дополнить такую раскраску до корректной.
| Название |
|---|




