| Codeforces Round 250 (Div. 2) |
|---|
| Закончено |
Конечно, наш ребенок любит гулять по зоопарку. В зоопарке n вольеров, пронумерованных от 1 до n. В i-м вольере содержится ai животных. Также в зоопарке имеется m дорог, каждая дорога соединяет два различных вольера. Естественно, зоопарк связный, так что до любого вольера можно дойти по дорожкам от любого другого вольера.
Наш ребенок очень умный. Предположим, что ребенок хочет пройти из вольера p в вольер q. Сначала он рассматривает все простые пути от p до q. Для каждого пути ребенок выписывает число, равное минимальному количеству животных в вольерах на этом пути. Обозначим наибольшее записанное число как f(p, q). Наконец, ребенок выбирает один из путей, для которого выписанное значение равно f(p, q).
Ребенок уже посетил зоопарк, и теперь он размышляет: чему равно среднее значение f(p, q) для всех пар p, q (p ≠ q)? Можете ли вы ответить на его вопрос?
В первой строке записано два целых числа, n и m (2 ≤ n ≤ 105; 0 ≤ m ≤ 105). Во второй строке записано n целых чисел: a1, a2, ..., an (0 ≤ ai ≤ 105). Затем следуют m строк, каждая строка содержит два целых числа, xi и yi (1 ≤ xi, yi ≤ n; xi ≠ yi), обозначающих дорогу между вольерами xi и yi.
Все дороги двусторонние, каждая пара вольеров соединена не более чем одной дорогой.
Выведите вещественное число — значение 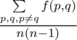 .
.
Ответ будет считаться правильным, если его относительная или абсолютная погрешность не превышает 10 - 4.
4 3
10 20 30 40
1 3
2 3
4 3
16.666667
3 3
10 20 30
1 2
2 3
3 1
13.333333
7 8
40 20 10 30 20 50 40
1 2
2 3
3 4
4 5
5 6
6 7
1 4
5 7
18.571429
Рассмотрим первый пример. Существует 12 возможных пар вольеров:
- p = 1, q = 3, f(p, q) = 10.
- p = 2, q = 3, f(p, q) = 20.
- p = 4, q = 3, f(p, q) = 30.
- p = 1, q = 2, f(p, q) = 10.
- p = 2, q = 4, f(p, q) = 20.
- p = 4, q = 1, f(p, q) = 10.
Еще 6 случаев симметричны приведенному выше. Среднее значение равно 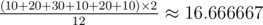 .
.
Рассмотрим второй пример. Существует 6 возможных пар вольеров:
- p = 1, q = 2, f(p, q) = 10.
- p = 2, q = 3, f(p, q) = 20.
- p = 1, q = 3, f(p, q) = 10.
Еще 3 случая симметричны приведенному выше. Среднее значение равно 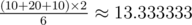 .
.
| Название |
|---|




