| Codeforces Round 268 (Div. 1) |
|---|
| Закончено |
У Little X есть дерево, состоящее из n вершин, пронумерованных от 1 до n. Для каждого ребра дерева задана его длина — целое положительное число. Определим расстояние между двумя вершинами v и u (обозначим его как d(v, u)) как сумму длин ребер в кратчайшем пути между v и u.
Будем называть перестановкой p последовательность из n различных целых чисел p1, p2, ..., pn (1 ≤ pi ≤ n). Little X хочет найти такую перестановку p, что сумма 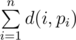 принимает как можно большее значение. При этом, если есть несколько оптимальных перестановок, он хочет найти лексикографически минимальную. Помогите ему найти такую перестановку!
принимает как можно большее значение. При этом, если есть несколько оптимальных перестановок, он хочет найти лексикографически минимальную. Помогите ему найти такую перестановку!
В первой строке записано целое число n (1 ≤ n ≤ 105).
В каждой из следующих n - 1 строк записано три целых числа через пробел ui, vi, wi (1 ≤ ui, vi ≤ n; 1 ≤ wi ≤ 105), обозначающих ребро между вершинами ui и vi с длиной, равной wi.
Гарантируется, что заданный граф является деревом.
В первой строке выведите максимально возможное значение описанной суммы. Во второй строке выведите n целых чисел — искомая лексикографически минимальная перестановка.
2
1 2 3
6
2 1
5
1 2 2
1 3 3
2 4 4
2 5 5
32
2 1 4 5 3
| Название |
|---|




