| Bayan 2015 Contest Warm Up |
|---|
| Закончено |
Представим город из n перекрестков и m улиц. Перекрестки пронумерованы от 1 до n.
Чтобы снизить количество заторов, мэр города решил сделать каждую улицу односторонней. Это значит, что на улице между перекрестками u и v машины могут ехать либо только от u до v, либо только от v до u.
Требуется так распределить направление дорожного движения на улицах, чтобы максимизировать количество пар (u, v), где 1 ≤ u, v ≤ n и можно достичь перекрёстка v, двигаясь из u, и проезжая по улицам в указанном направлении. Ваша задача — найти максимальное возможное количество таких пар.
В первой строке записаны числа n и m, (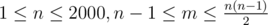 ), — количество перекрестков и улиц в городе соответственно.
), — количество перекрестков и улиц в городе соответственно.
В каждой из следующих m строк записано по два целых числа u и v, (u ≠ v), — конечные точки очередной улицы города.
Между каждой парой перекрестков проходит не больше одной улицы. Гарантируется, что до решения мэра (когда все улицы ещё были двусторонними) было возможно добраться от любого перекрестка до любого другого.
Выведите максимальное количество пар (u, v), таких, что можно достичь перекрестка v из u после распределения направления на улицах.
5 4
1 2
1 3
1 4
1 5
13
4 5
1 2
2 3
3 4
4 1
1 3
16
2 1
1 2
3
6 7
1 2
2 3
1 3
1 4
4 5
5 6
6 4
27
В первом примере если мэр сделает первую и вторую улицу односторонними в сторону перекрестка 1, а третью и четвертую улицы — в противоположную сторону, то будет 13 пар достижимых перекрестков: {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (2, 1), (3, 1), (1, 4), (1, 5), (2, 4), (2, 5), (3, 4), (3, 5)}
| Название |
|---|




