| Codeforces Beta Round 47 |
|---|
| Закончено |
Школьник Петя изучает квадратные уравнения. Уравнения, которые дают в школе, обычно имеют простой вид:
Петя заметил, что некоторые уравнения имеют два вещественных корня, некоторые только один, а некоторые уравнения вообще не имеют вещественных корней. Более того, оказалось, что несколько различных квадратных уравнений могут иметь общий корень.
Пете интересно, сколько вообще различных вещественных корней имеют все уравнения вышеописанного вида для всевозможных пар чисел b и c таких, что 1 ≤ b ≤ n, 1 ≤ c ≤ m. Помогите Пете узнать это число.
В единственной строке записаны два целых числа n и m. (1 ≤ n, m ≤ 5000000).
Выведите одно целое число — количество различных вещественных корней описанного семейства уравнений.
3 3
12
1 2
1
Во втором тесте из условия рассматриваются уравнения:
b = 1, c = 1: x2 + 2x + 1 = 0; Корень x = - 1
b = 1, c = 2: x2 + 2x + 2 = 0; Корней нет
Всего один корень.
В первом тесте рассматриваются уравнения:
b = 1, c = 1: x2 + 2x + 1 = 0; Корень x = - 1
b = 1, c = 2: x2 + 2x + 2 = 0; Корней нет
b = 1, c = 3: x2 + 2x + 3 = 0; Корней нет
b = 2, c = 1: x2 + 4x + 1 = 0; Корни 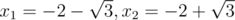
b = 2, c = 2: x2 + 4x + 2 = 0; Корни 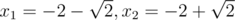
b = 2, c = 3: x2 + 4x + 3 = 0; Корни x1 = - 3, x2 = - 1
b = 3, c = 1: x2 + 6x + 1 = 0; Корни 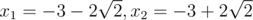
b = 3, c = 2: x2 + 6x + 2 = 0; Корни 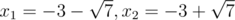
b = 3, c = 3: x2 + 6x + 3 = 0; Корни 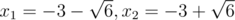
Всего корней 13, и поскольку корень - 1 повторяется дважды, то различных из них 12.
| Название |
|---|




