| Codeforces Round 285 (Div. 2) |
|---|
| Закончено |
Назовем суммой двух перестановок p и q чисел 0, 1, ..., (n - 1) перестановку 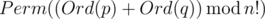 , где Perm(x) есть x-я лексикографически перестановка чисел 0, 1, ..., (n - 1) (в нумерации с нуля), а Ord(p) это номер перестановки p в лексикографическом порядке.
, где Perm(x) есть x-я лексикографически перестановка чисел 0, 1, ..., (n - 1) (в нумерации с нуля), а Ord(p) это номер перестановки p в лексикографическом порядке.
Например, Perm(0) = (0, 1, ..., n - 2, n - 1), Perm(n! - 1) = (n - 1, n - 2, ..., 1, 0)
У Миши есть две перестановки p и q. Ваша задача — найти их сумму.
По определению, перестановка a = (a0, a1, ..., an - 1) лекскикографически меньше перестановки b = (b0, b1, ..., bn - 1), если для некоторого k верно a0 = b0, a1 = b1, ..., ak - 1 = bk - 1, ak < bk.
В первой строке находится натуральное число n (1 ≤ n ≤ 200 000).
Во второй строке находятся n различных целых чисел от 0 до n - 1, разделённых пробелами, образующих перестановку p.
В третьей строке находятся n различных целых чисел от 0 до n - 1, разделённых пробелами, образующих перестановку q.
Выведите n различных целых чисел от 0 до n - 1, образующих сумму данных перестановок. Числа разделяйте пробелами.
2
0 1
0 1
0 1
2
0 1
1 0
1 0
3
1 2 0
2 1 0
1 0 2
Перестановки чисел от 0 до 1 в лексикографическом порядке: (0, 1), (1, 0).
В первом примере Ord(p) = 0 и Ord(q) = 0, значит ответ — это 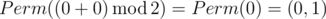 .
.
Во втором примере Ord(p) = 0 и Ord(q) = 1, значит ответ — это 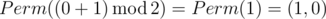 .
.
Перестановки чисел от 0 до 2 в лексикографическом порядке: (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1), (2, 1, 0).
В третьем примере Ord(p) = 3 и Ord(q) = 5, значит ответ — это 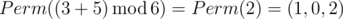 .
.
| Название |
|---|




