У Васи было два массива, составленных из целых неотрицательных чисел: a размера n и b размера m. Вася выбрал натуральное число k и построил таблицу v размера n × m по следующему правилу:
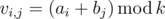
Вася записал таблицу v на листок и положил в стол.
Спустя год Вася, копаясь в кипе вещей в столе, нашёл какой-то листок, на котором была записана таблица w размера n × m. Он вспомнил, что когда-то давно строил таблицу по вышеописанным правилам, но он не уверен, что нашёл тот самый листок с таблицей v. Ваша задача — выяснить, могла ли найденная таблица w быть получена по этим правилам, и если да, то определить какой-нибудь набор чисел k, a1, a2, ..., an, b1, b2, ..., bm, по которым могла полуиться такая таблица.
В первой строке заданы натуральные числа n и m (1 ≤ n, m ≤ 100), разделенные пробелом — количество строк и столбцов в найденной таблице соответственно.
В i-й из последующих строк следуют числа wi, 1, wi, 2, ..., wi, m (0 ≤ wi, j ≤ 109), разделенные пробелами — элементы i-й строки таблицы w.
Если таблица w не могла быть получена указанным в условии способом, в единственной строке выведите «NO» (без кавычек).
Иначе нужно вывести четыре строки.
В первой строке выведите «YES» (без кавычек).
Во второй строке выведите натуральное число k (1 ≤ k ≤ 1018). Обратите внимание, что каждый элемент таблицы w должен лежать в пределах от 0 до k - 1 включительно.
В третьей строке выведите n натуральных чисел a1, a2, ..., an (0 ≤ ai ≤ 1018).
В четвертой строке выведите m натуральных чисел b1, b2, ..., bm (0 ≤ bi ≤ 1018).
2 3
1 2 3
2 3 4
YES
1000000007
0 1
1 2 3
2 2
1 2
2 0
YES
3
0 1
1 2
2 2
1 2
2 1
NO
Под записью 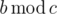 подразумевается остаток от целочисленного деления b на c.
подразумевается остаток от целочисленного деления b на c.
Гарантируется, что если существует какой-то набор чисел k, a1, ..., an, b1, ..., bm, по которому могла быть построена таблица w, то существует и набор чисел, удовлетворяющий ограничениям 1 ≤ k ≤ 1018, 1 ≤ ai ≤ 1018, 1 ≤ bi ≤ 1018. Иными словами, эти верхние границы введены только для удобства проверки.
| Название |
|---|




