| Codeforces Round 290 (Div. 1) |
|---|
| Закончено |
Лиса Ciel разработала игру-головоломку под названием «Многоугольник». В эту игру играют, используя триангуляции правильного n-угольника. Цель игры — преобразовать одну триангуляцию в другую, согласно определенным правилам.
Триангуляция n-угольника — это набор из n - 3 диагоналей, удовлетворяющих условию, что никакие две диагонали не имеют общих внутренних точек.
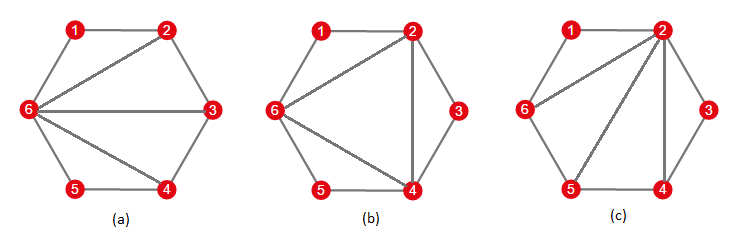
Например, изначальное состояние игры может выглядеть как (a) на рисунке, данном выше, а требуемое может выглядеть как (c). На каждом шагу вы можете выбрать диагональ триангуляции (но не ребро!) и инвертировать эту диагональ. Объясним, что значит инвертировать.
Допустим, вы хотите инвертировать диагональ a – b. Есть два треугольника со стороной a – b, обозначим их как a – b – c и a – b – d. В результате этой операции диагональ a – b заменяется диагональю c – d. Легко доказать, что после операции инвертирования получившийся набор диагоналей остается триангуляцией данного многоугольника.
Итак, чтобы решить приведенную выше задачу, можно сперва инвертировать диагональ 6 – 3, заменив её на диагональ 2 – 4. Затем можно инвертировать диагональ 6 – 4 и получить в результате рисунок (c).
Ciel только что доказала, что для любой начальной и конечной триангуляции у этой головоломки есть решение. Она хочет, чтобы вы решили задачу не более, чем за 20 000 шагов при условии n ≤ 1000.
В первой строке записано целое число n (4 ≤ n ≤ 1000), количество ребер правильного многоугольника.
Затем следуют две группы из (n - 3) строк, описывающих изначальную триангуляцию и конечную триангуляцию.
Описание каждой триангуляции состоит из (n - 3) строк. В каждой строке записано по 2 целых числа, ai и bi (1 ≤ ai, bi ≤ n), описывающих диагональ ai – bi.
Гарантируется, что и начальная, и конечная триангуляция корректны (то есть, никакие две диагонали не имеют общих внутренних точек в каждой из двух триангуляций).
Сперва выведите целое число k (0 ≤ k ≤ 20, 000), количество шагов.
Затем выведите k строк, в каждой строке должно следовать 2 целых числа, ai и bi — концы диагонали, которую вы хотите инвертировать на шаге номер i. Между собой ai и bi можно выводить в любом порядке.
Если есть несколько возможных решений, выведите любое из них.
4
1 3
2 4
1
1 3
6
2 6
3 6
4 6
6 2
5 2
4 2
2
6 3
6 4
8
7 1
2 7
7 3
6 3
4 6
6 1
6 2
6 3
6 4
6 8
3
7 3
7 2
7 1
Второй пример из условия обсуждается выше и показан на картинке.
| Название |
|---|




