| Codeforces Round 292 (Div. 2) |
|---|
| Закончено |
Drazil — это обезьяна. Он живет в парке круглой формы. Вокруг парка высажено n деревьев. Расстояние от i-го дерева до (i + 1)-го равняется di, расстояние от n-го дерева до первого дерева равняется dn. Высота i-го дерева равняется hi.
Drazil начинает каждый день с утренней пробежки. Утренняя пробежка состоит из следующих шагов:
- Drazil выбирает два различных дерева;
- Сперва он забирается на первое дерево;
- Затем он слезает с первого дерева, бежит вокруг парка (в одном из двух возможных направлений) ко второму дереву и забирается на него;
- Наконец, он слезает со второго дерева;
Но с недавнего времени рядом с некоторым множеством деревьев, образующим непрерывный отрезок, постоянно играют дети. Drazil терпеть не может детей, поэтому он не может выбирать деревья в близости от детей. Он даже не может перемещаться рядом с этими деревьями.
Если Drazil выберет два дерева x и y, то можно записать энергию, необходимую на утреннюю пробежку, как 2(hx + hy) + dist(x, y). Так как дети находятся на ровно одной из двух дуг, соединяющих x и y, то путь, по которому побежит Drazil, определяется однозначно, здесь за dist(x, y) обозначается его длина.
И вот, вы знаете, что на i-й день дети играют между ai-ым и bi-ым деревом. Более формально, если ai ≤ bi, то дети играют вокруг деревьев с индексами в диапазоне [ai, bi], в противном случае они играют вокруг деревьев с индексами в диапазоне 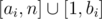 .
.
Пожалуйста, помогите Drazil для каждого дня определить, какие два дерева он должен выбрать, чтобы потратить как можно больше энергии (ведь он хочет быть крутой стройной обезьянкой) и посчитайте количество энергии, которое будет затрачено на утреннюю пробежку.
В первой строке следуют два целых числа, n и m (3 ≤ n ≤ 105, 1 ≤ m ≤ 105), обозначающих количество деревьев и количество дней соответственно.
Во второй строке следуют n целых чисел d1, d2, ..., dn (1 ≤ di ≤ 109), расстояния между соседними деревьями.
В третьей строке следуют n целых чисел h1, h2, ..., hn (1 ≤ hi ≤ 109), высоты деревьев.
В каждой из следующих m строк следует по два целых числа, ai и bi (1 ≤ ai, bi ≤ n), описывающих каждый новый день. Гарантируется, что всегда есть не менее двух доступных для Drazil деревьев, свободных от детей.
Для каждого дня выведите ответ на отдельной строке.
5 3
2 2 2 2 2
3 5 2 1 4
1 3
2 2
4 5
12
16
18
3 3
5 1 4
5 1 4
3 3
2 2
1 1
17
22
11
| Название |
|---|




