| Codeforces Round 292 (Div. 1) |
|---|
| Закончено |
У Drazil много друзей. Некоторые из них счастливы, а некоторые несчастны. Drazil хочет, чтобы все его друзья были счастливы. Поэтому он придумал такой план.
Среди его друзей n юношей и m девушек. Пронумеруем их от 0 до n - 1 и 0 до m - 1 соответственно. В i-й день Drazil приглашает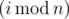 
-го юношу и 
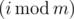-ю девушку поужинать (Drazil программист, поэтому i принимает значения с нуля). Если один из этих двух людей счастлив, то и другой становится счастливым. В противном случае оба человека останутся в том состоянии, в котором они были изначально. Как только человек становится счастливым (или же если он был счастлив с самого начала), он остается счастливым навсегда.
Drazil интересно, на какой день все его друзья станут счастливыми, если это вообще произойдёт. Помогите ему найти ответ на этот вопрос.
В первой строке следуют два целых числа n и m (1 ≤ n, m ≤ 109).
Во второй строке следует целое число b (0 ≤ b ≤ min(n, 105)), — количество счастливых парней среди друзей Drazil, затем следуют b различных целых чисел x1, x2, ..., xb (0 ≤ xi < n), — номера счастливых парней.
В третьей строке следует целое число g (0 ≤ g ≤ min(m, 105)), — количество счастливых девушек среди друзей Drazil, затем следуют g различных целых чисел y1, y2, ... , yg (0 ≤ yj < m), — номера счастливых девушек.
Гарантируется, что у Drazil есть не менее одного несчастного друга.
Выведите номер первого дня, когда все друзья Drazil станут счастливыми. Если этот день никогда не настанет, выведите -1.
2 3
0
1 0
4
2 4
1 0
1 2
-1
2 3
1 0
1 1
2
99999 100000
2 514 415
2 50216 61205
4970100515
Определим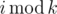 
как остаток от целочисленного деления i на k.
В первом тесте из условия:
- В 0-й день Drazil приглашает 0-го парня и 0-ю девушку. Так как 0-я девушка изначально счастливая, 0-й юноша становится счастлив в этот день.
- В 1-й день Drazil приглашает 1-го парня и 1-ю девушку. Они оба несчастны, так что в этот день ничего не меняется.
- Во 2-й день Drazil приглашает 0-го парня и 2-ю девушку. Так как 0-й парень уже счастлив, в этот день он делает 2-ю девушку счастливой.
- В 3-й день Drazil приглашает 1-го парня и 0-ю девушку. 0-я девушка счастливая, она делает счастливым 1-го парня.
- В 4-й день Drazil приглашает 0-го парня и 1-ю девушку. 0-ой парень счастлив, так что он делает 1-ю девушку счастливой. Итак, в этот момент все друзья Drazil становятся счастливыми.
