| Codeforces Round 298 (Div. 2) |
|---|
| Закончено |
В Берляндии вдоль главной улицы столицы курсирует автобус. Улица начинается от главной площади и представляет собой очень длинный отрезок. На протяжении всей улицы стоит n остановок, i-я из них расположена на расстоянии ai от центральной площади, все расстояния различны, остановки пронумерованы по возрастанию удаленности от площади, то есть ai < ai + 1 для всех i от 1 до n - 1. Автобус начинает свой путь от первой остановки, проезжает остановки 2, 3 и так далее. Он доезжает до остановки с номером n, разворачивается и едет в обратную сторону до остановки 1, проезжая все промежуточные остановки в обратном порядке. После этого он опять начинает движение в сторону остановки n. В течение дня автобус безостановочно курсирует по такому маршруту.
Автобус оснащен берляндской системой локального позиционирования. Когда автобус проезжает через остановку, система фиксирует ее номер.
Одна из ключевых возможностей системы — она может отвечать на запросы о пройденном расстоянии автобуса для участков его пути между некоторой парой остановок. Специальный модуль системы получает на вход информацию о наборе остановок на участке пути, причем номер остановки в наборе встречается столько раз, сколько раз мимо нее проехал автобус. Этот модуль возвращает длину пройденного участка пути (или -1, если длину однозначно определить невозможно). Работа модуля усложняется тем, что номера остановок передаются в запросе не в порядке их посещения, а в неубывающем порядке.
Например, если количество остановок равно 6, а участок пути автобуса начинается на остановке номер 5, заканчивается на остановке номер 3 и проходит остановки следующим образом: 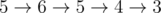 , то запрос об этом участке пути будет иметь вид: 3, 4, 5, 5, 6. Если же автобус на участке пути от остановки 5 до остановки 3 успевает проехать мимо 1-й остановки (то есть рассматривается участок, который заканчивается вторым посещением остановки 3 на пути из 5), то запрос будет иметь вид: 1, 2, 2, 3, 3, 4, 5, 5, 6.
, то запрос об этом участке пути будет иметь вид: 3, 4, 5, 5, 6. Если же автобус на участке пути от остановки 5 до остановки 3 успевает проехать мимо 1-й остановки (то есть рассматривается участок, который заканчивается вторым посещением остановки 3 на пути из 5), то запрос будет иметь вид: 1, 2, 2, 3, 3, 4, 5, 5, 6.
Вам предстоит повторить подвиг берляндских программистов и реализовать данную функцию.
В первой строке записано целое число n (2 ≤ n ≤ 2·105) — количество остановок.
Вторая строка содержит n целых чисел (1 ≤ ai ≤ 109) — расстояние i-й остановки от центральной площади. Числа во второй строке идут в порядке возрастания.
В третьей строке записано целое число m (1 ≤ m ≤ 4·105) — количество остановок, которые проехал автобус на некотором участке пути.
Четвертая строка содержит m целых чисел (1 ≤ bi ≤ n) — номера остановок, которые проехал автобус на участке пути, в отсортированном порядке. Номер остановки встречается такое количество раз, сколько раз ее проехал автобус.
Гарантируется, что запрос соответствует некоторому участку пути.
В единственную строку необходимо вывести расстояние, которое проехал автобус. Если это невозможно однозначно определить, необходимо вывести - 1.
6
2 3 5 7 11 13
5
3 4 5 5 6
10
6
2 3 5 7 11 13
9
1 2 2 3 3 4 5 5 6
16
3
10 200 300
4
1 2 2 3
-1
3
1 2 3
4
1 2 2 3
3
Первый тест из условия демонстрирует первый, разобранный в условии задачи пример.
Второй тест из условия демонстрирует второй, разобранный в условии задачи пример.
В третьем примере возможны два разных маршрута, которые имеют разные длины, следовательно, искомая длина участка не определена однозначно.
В четвертом примере, несмотря на то, что запросу соответствуют два разных маршрута, они имеют одинаковые длины, следовательно, искомая длина участка определена однозначно.
| Название |
|---|




