Недавно Леонид узнал об идемпотентных функциях. Идемпотентной функцией на множестве {1, 2, ..., n} называется такая функция 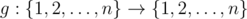 , что для любого
, что для любого 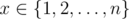 выполнено тождество g(g(x)) = g(x).
выполнено тождество g(g(x)) = g(x).
Обозначим за f(k)(x) результат k-кратного применения функции f к элементу x. Более формально, f(1)(x) = f(x), f(k)(x) = f(f(k - 1)(x)) для k > 1.
Дана некоторая функция 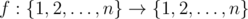 . Требуется найти такое минимальное положительное целое k, что функция f(k)(x) — идемпотентная.
. Требуется найти такое минимальное положительное целое k, что функция f(k)(x) — идемпотентная.
В первой строке входных данных следует целое число n (1 ≤ n ≤ 200) — количество элементов в области определения функции f.
Во второй строке следуют через пробел числа f(1), f(2), ..., f(n) (1 ≤ f(i) ≤ n для всех 1 ≤ i ≤ n) — значения функции.
Выведите такое минимальное k, что функция f(k)(x) — идемпотентная.
4
1 2 2 4
1
3
2 3 3
2
3
2 3 1
3
В первом тесте из условия функция f(x) = f(1)(x) уже является идемпотентной, так как f(f(1)) = f(1) = 1, f(f(2)) = f(2) = 2, f(f(3)) = f(3) = 2, f(f(4)) = f(4) = 4.
Второй тест из условия устроен следующим образом:
- функция f(x) = f(1)(x) не является идемпотентной, так как, например, f(f(1)) = 3, при этом f(1) = 2;
- функция f(x) = f(2)(x) является идемпотентной, так как для неё выполнено тождество f(2)(x) = 3, а значит и f(2)(f(2)(x)) = 3.
Третий тест из условия устроен следующим образом:
- функция f(x) = f(1)(x) не является идемпотентной, так как, например, f(f(1)) = 3, при этом f(1) = 2;
- функция f(f(x)) = f(2)(x) не является идемпотентной, так как, например, f(2)(f(2)(1)) = 2, при этом f(2)(1) = 3;
- функция f(f(f(x))) = f(3)(x) является идемпотентной, так как она тождественная: f(3)(x) = x для любого
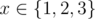 , а значит тождество f(3)(f(3)(x)) = f(3)(x) также выполнено.
, а значит тождество f(3)(f(3)(x)) = f(3)(x) также выполнено.
| Название |
|---|




