| Codeforces Round 316 (Div. 2) |
|---|
| Закончено |
Как-то Миша и Андрей играли в очень простую игру. Сначала каждый игрок выбирает целое число в пределах от 1 до n. Пусть Миша выбрал число m, а Андрей — число a.
Затем с помощью генератора случайных чисел выбирается случайное целое число c в пределах от 1 до n (любое целое число от 1 до n может быть выбрано с одной и той же вероятностью), после чего побеждает тот игрок, чьё число оказалось ближе к c. Ребята договорились, что в случае, когда m и a находятся на одинаковом расстоянии от c, выигрывает Миша.
Андрей хочет победить любой ценой и просит вас помочь ему. Вам известно число, выбранное Мишей, и число n. Нужно определить, какое число a, должен выбрать Андрей, чтобы вероятность его победы была максимальной.
Более формально, нужно найти такое целое число a (1 ≤ a ≤ n), чтобы вероятность того, что 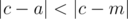 , была максимальна, где c — выбранное равновероятно случайное целое число от 1 до n (включительно).
, была максимальна, где c — выбранное равновероятно случайное целое число от 1 до n (включительно).
В первой строке находятся два целых числа n и m (1 ≤ m ≤ n ≤ 109) — диапазон чисел в игре и выбранное Мишей число соответственно.
Выведите одно целое число — такое значение a, чтобы вероятность победы Андрея была максимальной. Если таких значений несколько, выведите минимальное из них.
3 1
2
4 3
2
В первом тесте: Андрей победит если c равно 2 или 3. Вероятность победы Андрея равна 2 / 3. Если Андрей выберет число a, равное 3, то вероятность победы будет 1 / 3. При a, равном 1, вероятность победы — 0.
Во втором тесте: Андрей победит если c равно 1 или 2. Вероятность победы Андрея — 1 / 2. При остальных вариантах выбора a вероятность победы меньше.
| Название |
|---|




