Вам дана зеркальная коробка. Коробка представляет собой сетку размера n × m. Каждая ячейка сетки содержит зеркало, расположенное в форме '\' или ' / ' (т. е. под 45 градусов к горизональной или вертикальной прямой). Но, к сожалению, некоторые ячейки содержат разбитые зеркала. Вы хотите поместить новые зеркала в эти ячейки таким образом, чтобы выполнялись следующие два условия:
- Если пустить луч света горизонтально/вертикально в середину любого единичного отрезка, являющегося стороной некоторой граничной ячейки, то луч света выйдет из одноги из соседних с ним единичных отрезков.
- Каждый единичный отрезок сетки, образующей коробку с зеркалами, может быть достигнут лучом света, пущенным в соответствие с правилами из предыдущего абзаца.
Когда вы попробовали вставить несколько зеркал, вы обнаружили, что это можно сделать многими способами. Сколько существует возможных способов вставить зеркала на разбитые места, удовлетворяя условию задачи? Ответ может быть большим, поэтому выведите остаток от его деления на простое число MOD.
В первой строке записано три целых числа n, m (1 ≤ n, m ≤ 100), размеры коробки и MOD (2 ≤ MOD ≤ 109 + 7, MOD — простое число) — модуль, по которому надо посчитать ответ.
В каждой из следующих n строк записана строка длины m. Каждая строка содержит символы ' / ', '\', '*', где '*' обозначает, что зеркало в этой ячейке разбито.
Гарантируется, что количество '*' не превышает 200.
Выведите ответ по модулю MOD.
2 2 1000000007
*/
/*
1
2 2 1000000007
**
\\
1
2 2 3
**
**
2
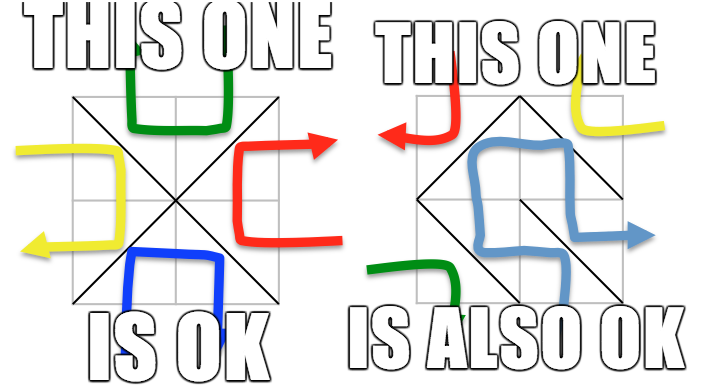
Единственный способ для первого примера показан на левой картинке в условии.
Единственный способ для второго примера показаны на правой картинке в условии.
Для третьего примера есть 5 возможностей, приведенных ниже:
1.
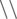
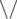
2.
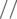
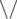
3.

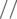
4.

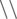
5.
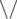

| Название |
|---|




