| Codeforces Round 326 (Div. 1) |
|---|
| Закончено |
Duff — королева своей страны, Andarz Gu. Она — поклоннца спортивного программирования. Поэтому, увидев своего министра Malek'а без дела, она дала ему последовательность, состоящую из n неотрицательных целых чисел a1, a2, ..., an и попросила его выполнить q запросов для неё на этой последовательности.

Дано два типа запросов:
- даны числа l, r и k, Malek должен произвести
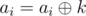 для каждого l ≤ i ≤ r (
для каждого l ≤ i ≤ r (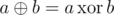 , побитовое исключающее ИЛИ чисел a и b)
, побитовое исключающее ИЛИ чисел a и b) - даны числа l и r, Malek длжен назвать королеве качество данной последовательности al, al + 1, ... , ar.
качеством последовательности b1, ..., bk называется количество её Kheshtak'ов. Неотрицательное целое числа w является Kheshtak'ом последовательности тогда и только тогда, когда у неё есть подпоследовательность bi1, bi2, ..., bix (возможно, пустая), такая, что 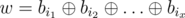 (1 ≤ i1 < i2 < ... < ix ≤ k). Если эта подпоследовательнось пустая, то w полагается равным нулю.
(1 ≤ i1 < i2 < ... < ix ≤ k). Если эта подпоследовательнось пустая, то w полагается равным нулю.
В отличие от Duff, Malek — не программист. Поэтому он попросил вас о помощи. Пожалуйста, помогите ему выполнить эти запросы.
В первой строке ввода содержатся два целых числа, n и q (1 ≤ n ≤ 2 × 105 и 1 ≤ q ≤ 4 × 104).
Во второй строке ввода содержатся n целых чисел, a1, a2, ..., an через пробел (0 ≤ ai ≤ 109 для каждого 1 ≤ i ≤ n).
В следующих q строках содержатся запросы. Каждая строка начинается с целого числа t (1 ≤ t ≤ 2), обозначающего тип соответствующего запроса. Если t = 1, то далее следуют ещё три целых числа, l, r и k. В противном случае следуют ещё два целых числа, l и r. (1 ≤ l ≤ r ≤ n, и 0 ≤ k ≤ 109)
Выведите ответ на каждый запрос второго типа в своей строке.
5 5
1 2 3 4 2
2 1 5
1 2 2 8
2 1 5
1 1 3 10
2 2 2
8
16
1
В первом запросе нас интересуют все Kheshtak'и последовательности (1, 2, 3, 4, 2), их восемь штук и они 0, 1, 2, 3, 4, 5, 6, 7.
В третьем запросе нас интересуют все Kheshtak'и последовательности (1, 10, 3, 4, 2), их шестнадцать штук и они 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15.
В пятом запросе нас интересуют все Kheshtak'и последовательности (0). Единственный Khestak в данном случае равен 0.
| Название |
|---|




